
【题目】已知:如图所示,在△ABC中,∠B=90°,AB=5cm,BC=7cm.点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,当其中一点达到终点后,另外一点也随之停止运动.
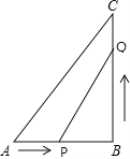
(1)如果P,Q分别从A,B同时出发,那么几秒后,△PBQ的面积等于4cm2?
(2)如果P,Q分别从A,B同时出发,那么几秒后,PQ的长度等于5cm?
(3)在(1)中,当P、Q出发几秒时,△PBQ的面积最大,最大面积是多少?
【答案】(1)1秒;(2)2秒;(3)![]() 秒后,△PBQ的面积最大,最大面积是
秒后,△PBQ的面积最大,最大面积是![]() cm2.
cm2.
【解析】
(1)设t秒后,△PBQ的面积等于4cm2,根据点P从A点开始沿AB边向点B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动,表示出BP和BQ的长可列方程求解;
(2)利用勾股定理列出方程求解即可;
(3)结合(1)列出函数关系式,化成顶点是即可.
解:(1)设t秒后,△PBQ的面积等于4cm2,
则:AP=tcm,BP=(5-t)cm; BQ=2tcm.
S△PBQ=![]() BP×BQ,即4=
BP×BQ,即4=![]() ×(5-t)×2t,
×(5-t)×2t,
解得:t=1或4.(t=4秒不合题意,舍去)
答:1秒后,△PBQ的面积等于4cm2;
(2)设t秒后,△PBQ中PQ的长度等于5cm,即PQ=5,
则PQ2=25=BP2+BQ2,即25=(5-t)2+(2t)2,
解得:t=0(舍)或2.
答:2秒后,PQ的长度为5cm;
(3)设面积为Scm2,时间为t,
则S =![]() BP×BQ=
BP×BQ=![]() ×(5-t)×2t =-t2+5t= -(t-
×(5-t)×2t =-t2+5t= -(t-![]() )2+
)2+![]() ,
,
答:![]() 秒后,△PBQ的面积最大,最大面积是
秒后,△PBQ的面积最大,最大面积是![]() cm2.
cm2.


 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:
【题目】解方程:(1) ![]() ; (2)
; (2)![]() .
.
【答案】(1)x1 =1 ,x2=![]() ; (2) x1 =-1,x2=
; (2) x1 =-1,x2=![]() .
.
【解析】试题分析:
根据两方程的特点,使用“因式分解法”解两方程即可.
试题解析:
(1)原方程可化为: ![]() ,
,
方程左边分解因式得: ![]() ,
,
![]() 或
或![]() ,
,
解得: ![]() ,
, ![]() .
.
(2)原方程可化为: ![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() 或
或![]() ,
,
解得: ![]() .
.
【题型】解答题
【结束】
20
【题目】已知x1,x2是关于x的一元二次方程x2-2(m+1)x+m2+5=0的两实根.
(1)若(x1-1)(x2-1)=28,求m的值;
(2)已知等腰△ABC的一边长为7,若x1,x2恰好是△ABC另外两边的边长,求这个三角形的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知顶点为(﹣3,﹣6)的抛物线y=ax2+bx+c经过点(﹣1,﹣4),则下列结论中错误的是( )
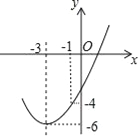
A. b2>4ac
B. ax2+bx+c≥﹣6
C. 若点(﹣2,m),(﹣5,n)在抛物线上,则m>n
D. 关于x的一元二次方程ax2+bx+c=﹣4的两根为﹣5和﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的顶点
的顶点![]() 是直线
是直线![]() 和直线
和直线![]() 的交点.
的交点.
(1)用含![]() 的代数式表示顶点
的代数式表示顶点![]() 的坐标.
的坐标.
(2)①当![]() 时,
时,![]() 的值均随
的值均随![]() 的增大而增大,求
的增大而增大,求![]() 的取值范围.
的取值范围.
②若![]() ,且
,且![]() 满足
满足![]() 时,二次函数的最小值为
时,二次函数的最小值为![]() ,求
,求![]() 的取值范围.
的取值范围.
(3)试证明:无论![]() 取任何值,二次函数
取任何值,二次函数![]() 的图象与直线
的图象与直线![]() 总有两个不同的交点.
总有两个不同的交点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某日上午7:00,一列火车在A城的正北24km处,以12km/h的速度驶向A城.同时,一辆汽车在A城的正东12km处,以12km/h的速度驶向正西方向行驶.假设火车和汽车的行驶的方向和速度都保持不变.
问:(1)何时火车与汽车之间的距离最近?最近距离是多少千米?
(2)当火车与汽车之间的距离最近时,汽车是否已过铁路与公路的立交处?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ABC=∠BCD=90°,点E为BC的中点,AE⊥DE.
(1)求证:△ABE∽△ECD;
(2)求证:AE2=AB·AD;
(3)若AB=1,CD=4,求线段AD,DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有两张完全重合的矩形纸片,将其中一张绕点A顺时针旋转90°后得到矩形AMEF(如图1),连接BD,MF,若BD=4cm,∠ADB=30°.
(1)试探究线段BD与线段MF的数量关系和位置关系,并说明理由;
(2)把△BCD与△MEF剪去,将△ABD绕点A顺时针旋转得△AB1D1,边AD1交FM于点K(如图2),设旋转角为β(0°<β<90°),当△AFK为等腰三角形时,求β的度数.
(3)若将△AFM沿AB方向平移得到△A2F2M2(如图3),F2M2与AD交于点P,A2M2与BD交于点N,当NP∥AB时,求平移的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知矩形AOCB,AB=6cm,BC=16cm,动点P从点A出发,以3cm/s的速度向点O运动,直到点O为止;动点Q同时从点C出发,以2cm/s的速度向点B运动,与点P同时结束运动.
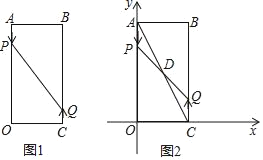
(1)当运动时间为2s时,P、Q两点的距离为 cm;
(2)请你计算出发多久时,点P和点Q之间的距离是10cm;
(3)如图2,以点O为坐标原点,OC所在直线为x轴,OA所在直线为y轴,1cm长为单位长度建立平面直角坐标系,连结AC,与PQ相交于点D,若双曲线![]() 过点D,问k的值是否会变化?若会变化,说明理由;若不会变化,请求出k的值.
过点D,问k的值是否会变化?若会变化,说明理由;若不会变化,请求出k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
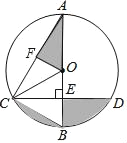
【题目】如图,AB为⊙O的直径,CD是弦,AB⊥CD于点E,OF⊥AC于点F,BE=OF.
(1)求证:△AFO≌△CEB;
(2)若BE=4,CD=8![]() ,求:
,求:
①⊙O的半径;
②求图中阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com