
 如图,直线y=2x+2与x轴交于点A,与y轴交于点B.
如图,直线y=2x+2与x轴交于点A,与y轴交于点B.| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
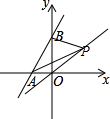 解:(1)当y=0时,2x+2=0,解得x=-1,则A点坐标为(-1,0);
解:(1)当y=0时,2x+2=0,解得x=-1,则A点坐标为(-1,0);| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| b |
| k |


科目:初中数学 来源: 题型:
 如图,在梯形ABCD中,∠ABC=90°,AE∥CD交BC于E,O是AC的中点,AB=
如图,在梯形ABCD中,∠ABC=90°,AE∥CD交BC于E,O是AC的中点,AB=| 3 |
| A、1 | B、2 | C、3 | D、4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 根据程序设定,机器人在平面上能完成下列动作:如图,先从点O沿北偏东60°方向行走一段时间到点P后,立即再向正北方向行走一段时间到点Q.但何时改变方向不定,假设机器人行走速度为2m/min,机器人行走3min时到达的位置为点Q.
根据程序设定,机器人在平面上能完成下列动作:如图,先从点O沿北偏东60°方向行走一段时间到点P后,立即再向正北方向行走一段时间到点Q.但何时改变方向不定,假设机器人行走速度为2m/min,机器人行走3min时到达的位置为点Q.| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 星期 | 一 | 二 | 三 | 四 | 五 |
| 每股涨跌 | +0.3 | +0.1 | -0.2 | -0.5 | +0.2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com