
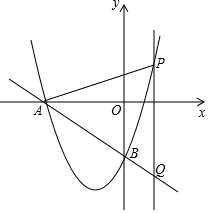
 ��ͼ����ֱ֪��l��y=-$\frac{3}{4}$x-3��x�ύ�ڵ�A����y�ύ�ڵ�B��������y=ax2+bx+c����A��B���㣬�ҶԳ���Ϊֱ��x=-$\frac{3}{2}$��
��ͼ����ֱ֪��l��y=-$\frac{3}{4}$x-3��x�ύ�ڵ�A����y�ύ�ڵ�B��������y=ax2+bx+c����A��B���㣬�ҶԳ���Ϊֱ��x=-$\frac{3}{2}$������ ��1�����A��B�������꣬���������鼴�ɽ�����⣮
��2������Q������Ϊ����x��-$\frac{3}{4}$x-3������A��-4��0����B��0��-3�����Ƴ�AB=$\sqrt{{4}^{2}+{3}^{2}}$=5��AB���е�����Ϊ��-2��-$\frac{3}{2}$������Ϊ��ABΪֱ����Բǡ����ֱ��PQ���У��ɵ�|x-��-2��|=$\frac{5}{2}$���ⷽ�̼��ɽ�����⣮
�ڷ��������Σ��ֱ����̼��ɽ�����⣮
��� �⣺��1����ֱ��l��y=-$\frac{3}{4}$x-3��x�ύ�ڵ�A����y�ύ�ڵ�B��
��A��-4��0����B��0��-3����
��������y=ax2+bx+c����A��B���㣬�ҶԳ���Ϊֱ��x=-$\frac{3}{2}$��
��$\left\{\begin{array}{l}{16a-4b+c=0}\\{c=-3}\\{-\frac{b}{2a}=-\frac{3}{2}}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{a=\frac{3}{4}}\\{b=\frac{9}{4}}\\{c=-3}\end{array}\right.$��
�������ߵĽ���ʽΪ��y=$\frac{3}{4}$x2+$\frac{9}{4}$x-3��
��2������Q����������x��-$\frac{3}{4}$x-3����
��A��-4��0����B��0��-3����
��AB=$\sqrt{{4}^{2}+{3}^{2}}$=5��AB���е�����Ϊ��-2��-$\frac{3}{2}$����
����ABΪֱ����Բǡ����ֱ��PQ���У�
��|x-��-2��|=$\frac{5}{2}$��
��ã�x=$\frac{1}{2}$��-$\frac{9}{2}$��
���ʱ��Q������Ϊ����$\frac{1}{2}$��-$\frac{27}{8}$����-$\frac{9}{2}$��$\frac{3}{8}$����
����P��������x��$\frac{3}{4}$x2+$\frac{9}{4}$x-3������Q��x��-$\frac{3}{4}x-3$��
��ͼ1�У���PA=PQʱ����PM��AQ��M����PQ��x����N����֪PQ=$\frac{3}{4}$x2+3x��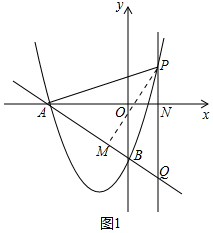
��OB��NQ��
��OA��AN=AB��AQ��
��4����4+x��=5��AQ��
��AQ=$\frac{5}{4}$��4+x����AM=MQ=$\frac{5}{8}$��4+x����
��cos��AQN=cos��PQM=$\frac{3}{5}$��
��$\frac{\frac{5}{8}��4+x��}{\frac{3}{4}{x}^{2}+3x}=\frac{3}{5}$��
���x=$\frac{25}{18}$��-4������������ʱQ��$\frac{25}{18}$��-$\frac{97}{24}$����
��ͼ2�У���QA=QPʱ������$\frac{5}{4}$��4+x��=$\frac{3}{4}$x2+3x�����x=$\frac{5}{3}$��-4������������ʱQ��$\frac{5}{3}$��-$\frac{17}{4}$����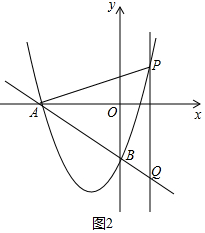
��ͼ3�У���AP=AQʱ����AP��y����N��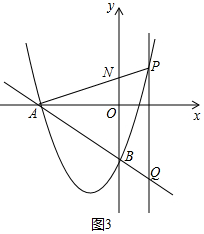
��ֱ��AP��ֱ��AQ����x��Գƣ�
��N��0��3����
��ֱ��AN�Ľ���ʽΪy=$\frac{3}{4}$x+3��
��$\left\{\begin{array}{l}{y=\frac{3}{4}x+3}\\{y=\frac{3}{4}{x}^{2}+\frac{9}{4}x-3}\end{array}\right.$���$\left\{\begin{array}{l}{x=-4}\\{y=0}\end{array}\right.$��$\left\{\begin{array}{l}{x=2}\\{y=\frac{9}{2}}\end{array}\right.$��
��A��-4��0����
��P��2��$\frac{9}{2}$����
��Q��2��-$\frac{9}{2}$����
�������������������ĵ�Q������Ϊ��$\frac{25}{18}$��-$\frac{97}{24}$����$\frac{5}{3}$��-$\frac{17}{4}$����2��-$\frac{9}{2}$����
���� ���⿼����κ����ۺ��⡢����ϵ���������������ε��ж������ʡ�һԪ���η��̵�֪ʶ������Ĺؼ������������ѧ֪ʶ��ѧ���÷������۵�˼��˼�����⣬ѧ�ṹ�����̽�����⣬�����п�ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
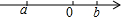 ��������ʵ��a��b��λ����ͼ��ʾ������|a+b|+$\sqrt{��a-b��^{2}}$�Ľ���ǣ�������
��������ʵ��a��b��λ����ͼ��ʾ������|a+b|+$\sqrt{��a-b��^{2}}$�Ľ���ǣ�������| A�� | -2a-b | B�� | -2a+b | C�� | -2b | D�� | -2a |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{{{��{-4}��}^2}}=-4$ | B�� | ��a2��3=a5 | C�� | 2a-a=2 | D�� | a•a3=a4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com