【题目】如图，∠AOC：∠COD：∠BOD=2：3：4，且A，O，B三点在一条直线上，OE，OF分别平分∠AOC和∠BOD，OG平分∠EOF，求∠GOF的度数。
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】在求两位数的平方时，可以用“列竖式”的方法进行速算，求解过程如图1所示．仿照图1，用“列竖式”的方法计算一个两位数的平方，部分过程如图2所示，若这个两位数的个位数字为a，则这个两位数为（ ）
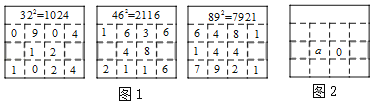
A.a﹣50B.a+50C.a﹣20D.a+20
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（大丰某校数学兴趣小组活动场景）
（课堂再现）
师：同学们还记得教材P43分配律a（b+c）=ab+ac吗？现在，老师和大家一起来用几何的方法来证明这个公式。相信今天会惊喜不断。（学生期待惊喜中………），
（教者呈现教具）老师手上有两个长方形，长分别是b、c，宽都是a，（如图1）它们各自面积是多少？
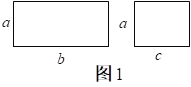
生1：面积分别为ab、ac。
师：现在我们把它们拼在一起（如图2），组成了一个新长方形，新长方形面积又是多少呢？
生2：
师：所以……
生3：所以得到
，也就是说
（真好玩！）
师：相信大家能用类似方法来推导一个我们暂时还没学习的公式，老师期待大家给我的惊喜哦！（屏幕上呈现问题）
（拓展延伸）
将边长为a的正方形纸板上剪去一个边长为b的正方形（如图3），将剩余的纸板沿虚线剪开，拼成如图4的梯形。
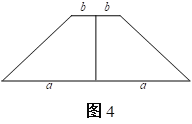
（1）你能得到一个什么等式.（用含a、b的式子表示）
（再接再厉）
（2）直接运用上面你发现的公式完成运算：
（拓展提高）
（3）直接运用上面你发现的公式解下列方程：
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】6张如图1的长为a，宽为b（a＞b）的小长方形纸片，按图2方式不重叠地放在矩形ABCD内，未被覆盖的部分（两个矩形）用阴影表示．设左上角与右下角的阴影部分的面积的差为S，当BC的长度变化时，按照同样的放置方式，S始终保持不变，则a，b满足（ ）
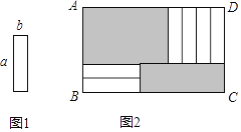
A. a=2b B. a=3b C. a=4b D. a=b
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某工厂车间为了了解工人日均生产能力的情况，随机抽取10名工人进行测试，将获得数据制成如下统计图.
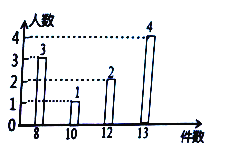
（1）求这10名工人的日均生产件数的平均数、众数、中位数；
（2）若日均生产件数不低于12件为优秀等级，该工厂车间共有工人120人，估计日均生产能力为“优秀”等级的工人约为多少人？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】甲、乙两人利用不同的交通工具，沿同一路线分别从A、B两地同时出发匀速前往C地（B在A、C两地的途中）．设甲、乙两车距A地的路程分别为y甲、y乙（千米），行驶的时间为x（小时），y甲、y乙与x之间的函数图象如图所示．
（1）直接写出y甲、y乙与x之间的函数表达式；
（2）如图，过点（1，0）作x轴的垂线，分别交y甲、y乙的图象于点M，N．求线段MN的长，并解释线段MN的实际意义；
（3）在乙行驶的过程中，当甲、乙两人距A地的路程差小于30千米时，求x的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某中学随机抽取部分学生进行科技知识的调查测试,测试成绩分为A,B,C,D,E五个等级,通过对测试成绩的分析,得到如下条形统计图:
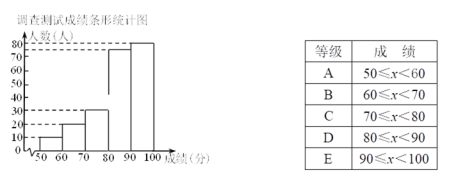
请根据所给信息,解答下列问题：
（1）试分析本次调查测试成绩的“中位数”在哪个等级；
（2）若本次调查测试成绩在80分及以上为优秀,该中学共有800人,请估计全校测试成绩为优秀的学生人数.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线l1，l2，l3分别过正方形ABCD的三个顶点A，D，C，且相互平行，若l1，l2的距离为2，l2，l3的距离为4，则正方形的对角线长为_______________．
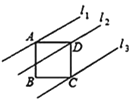
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】根据要求，解答下列问题：
（1）①方程x2﹣x﹣2=0的解为 ；
②方程x2﹣2x﹣3=0的解为 ；
③方程x2﹣3x﹣4=0的解为 ；
…
（2）根据以上方程特征及其解的特征，请猜想：
①方程x2﹣9x﹣10=0的解为 ；
②请用配方法解方程x2﹣9x﹣10=0，以验证猜想结论的正确性．
（3）应用：关于x的方程 的解为x1=﹣1，x2=n+1．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
