
分析 由a+b+c=1,得到(a+2)+(b+3)+(C+4)=10,两边平方后利用整体代入的思想解决问题.
解答 解:∵a+b+c=1,
∴(a+2)+(b+3)+(C+4)=10,
两边平方得:(a+2)2+(b+3)2+(c+4)2+2[(a+2)(b+3)+(a+2)(c+4)+(b+3)(c+4)]=100,
∵$\frac{1}{a+2}$+$\frac{1}{b+3}$$+\frac{1}{c+4}$=0,
∴(b+3)(c+4)+(a+2)(c+4)+(a+2)(b+3)=0,
∴(a+2)2+(b+3)2+(c+4)2=100.
故答案为100.
点评 本题考查分式的化简,解决问题的关键是利用公式巧妙变形,整体化简的思想,难度比较大,有一定的技巧性.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
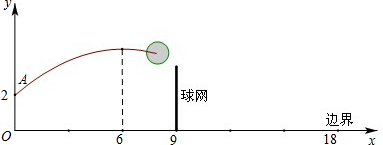
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
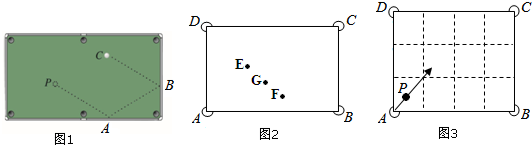
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com