
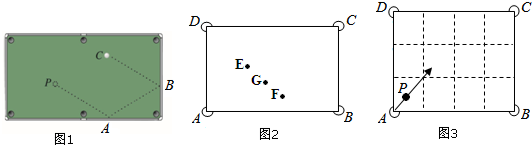
分析 (1)类似于光线的反射问题,可通过计算同旁内角互补,得出平行的结论;
(2)入射角等于反射角,找出E点关于AB的对称点E1,连接E1F交AB于H根据对称图形的特点及对顶角相等得出∠BHF=∠E1HA=∠EHA,求出E1N及NF的长运用勾股定理求出E1F的长,因对应边EH=E1H,E1H即为所求;
(3)根据当AB=4,AD=3时的例图及弹子的运行规律:每一条运行轨迹都是一个正方形的对角线,画出图形,即可得出结论.
解答 解:(1)如图,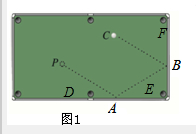
∵∠PAD=∠BAE,∠PAB=180°-∠PAD-∠BAE,
∴∠PAB=180°-2∠BAE.
同理,∠ABC=180°-2∠ABE.
∵∠BAE+∠ABE=90°,
∴∠PAB+∠ABC=360°-2(∠BAE+∠ABE)=180°.
∴BC∥PA.
(2)可作点E关于直线AB的对称点E1,连接E1F,E1F与AB交于点H,球E的运动路线就是EH→HF,
过点F作AB的平行线交E1E的延长线于点N,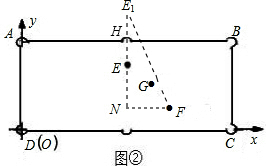 ;
;
(3)如图,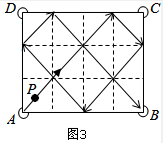
母球P从角落A以45°角击出,在桌子边缘回弹若干次后,最终必将落入B(填A、B、C、D)角落的球袋,在它落入球袋之前,与桌子边缘共回弹了5次;
设由DC边反弹,弹子撞击BC边的位置距离C点为K格,从BC边反弹后,弹子撞击AB边的位置距离B点为(99-k)格,距离A点为(k+1)格经过AB边反弹后,弹子撞击AD边的位置距离A点为(k+1)格,距离D点为[99-(K+1)]格,经AD反弹,弹子撞击DC边的位置距离D点为[99-(k+1)]格,距离C点为100-[99-(K+1)]=K+2格再撞击BC边的位置距离C点为k+2格,即比前一次的位置下移2格,所以要撞击边的次数为100+99-2=197次.
点评 此题考查作图-应用与实际作图,读懂题意,根据题意总结出弹子的运行规律,画出图形是解题的关键.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,AB⊥AC,CD平分∠ACB,BE平分∠ABC,AG∥BC,AG⊥BG.下列结论:①∠BAG=2∠ABF;②BA平分∠CBG;③∠ABG=2∠ACD;④∠ABE=∠ACD,其中正确的结论是( )
如图,AB⊥AC,CD平分∠ACB,BE平分∠ABC,AG∥BC,AG⊥BG.下列结论:①∠BAG=2∠ABF;②BA平分∠CBG;③∠ABG=2∠ACD;④∠ABE=∠ACD,其中正确的结论是( )| A. | ①③ | B. | ②④ | C. | ①②③ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在四边形ABCD中,已知∠ACB=∠BAD=105°,∠ABC=∠ADC=45°,则∠CAD的度数为( )
如图,在四边形ABCD中,已知∠ACB=∠BAD=105°,∠ABC=∠ADC=45°,则∠CAD的度数为( )| A. | 60° | B. | 70° | C. | 75° | D. | 80° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
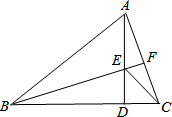 在△ABC中,AB=BC,∠ABC=45°,AD是BC边上的高,E是AD上一点,ED=CD,连接EC,求证:
在△ABC中,AB=BC,∠ABC=45°,AD是BC边上的高,E是AD上一点,ED=CD,连接EC,求证:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x2-70x+825=0 | B. | x2+70x-825=0 | C. | x2-140x+3300=0 | D. | x2+140x-3300=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
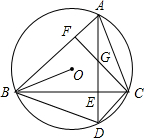 如图,△ABC内接于⊙O,弦AD⊥BC于E,CF⊥AB于F,交AD于G,BE=3,CE=2,且tan∠OBC=1,求四边ABDC的面积.
如图,△ABC内接于⊙O,弦AD⊥BC于E,CF⊥AB于F,交AD于G,BE=3,CE=2,且tan∠OBC=1,求四边ABDC的面积.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com