
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象交x轴于A、B两点,交y轴于点D,点B的坐标为(3,0),顶点C的坐标为(1,4).
(1)求二次函数的解析式和直线BD的解析式;
(2)点P是直线BD上的一个动点,过点P作x轴的垂线,交抛物线于点M,当点P在第一象限时,求线段PM长度的最大值;
(3)在抛物线上是否存在异于B、D的点Q,使△BDQ中BD边上的高为2 ![]() ?若存在求出点Q的坐标;若不存在请说明理由.
?若存在求出点Q的坐标;若不存在请说明理由.
【答案】
(1)
解:∵抛物线的顶点C的坐标为(1,4),
∴可设抛物线解析式为y=a(x﹣1)2+4,
∵点B(3,0)在该抛物线的图象上,
∴0=a(3﹣1)2+4,解得a=﹣1,
∴抛物线解析式为y=﹣(x﹣1)2+4,即y=﹣x2+2x+3,
∵点D在y轴上,令x=0可得y=3,
∴D点坐标为(0,3),
∴可设直线BD解析式为y=kx+3,
把B点坐标代入可得3k+3=0,解得k=﹣1,
∴直线BD解析式为y=﹣x+3
(2)
解:设P点横坐标为m(m>0),则P(m,﹣m+3),M(m,﹣m2+2m+3),
∴PM=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m=﹣(m﹣ ![]() )2+
)2+ ![]() ,
,
∴当m= ![]() 时,PM有最大值
时,PM有最大值 ![]()
(3)
解:如图,过Q作QG∥y轴交BD于点G,交x轴于点E,作QH⊥BD于H,

设Q(x,﹣x2+2x+3),则G(x,﹣x+3),
∴QG=|﹣x2+2x+3﹣(﹣x+3)|=|﹣x2+3x|,
∵△BOD是等腰直角三角形,
∴∠DBO=45°,
∴∠HGQ=∠BGE=45°,
当△BDQ中BD边上的高为2 ![]() 时,即QH=HG=2
时,即QH=HG=2 ![]() ,
,
∴QG= ![]() ×2
×2 ![]() =4,
=4,
∴|﹣x2+3x|=4,
当﹣x2+3x=4时,△=9﹣16<0,方程无实数根,
当﹣x2+3x=﹣4时,解得x=﹣1或x=4,
∴Q(﹣1,0)或(4,﹣5),
综上可知存在满足条件的点Q,其坐标为(﹣1,0)或(4,﹣5)
【解析】(1)可设抛物线解析式为顶点式,由B点坐标可求得抛物线的解析式,则可求得D点坐标,利用待定系数法可求得直线BD解析式;(2)设出P点坐标,从而可表示出PM的长度,利用二次函数的性质可求得其最大值;(3)过Q作QG∥y轴,交BD于点G,过Q和QH⊥BD于H,可设出Q点坐标,表示出QG的长度,由条件可证得△DHG为等腰直角三角形,则可得到关于Q点坐标的方程,可求得Q点坐标.


科目:初中数学 来源: 题型:
【题目】在一个不透明的布袋里装有4个标有1,2,3,4的小球,它们的形状、大小、质地完全相同,小李从布袋里随机取出一个小球,记下数字为x,小张在剩下的3个小球中随机取出一个小球,记下数字为y,这样确定了点Q的坐标(x,y).
(1)画树状图或列表,写出点Q所有可能的坐标;
(2)求点Q(x,y)在函数y=﹣x+5图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一艘渔船位于港口A的北偏东60°方向,距离港口20海里B处,它沿北偏西37°方向航行至C处突然出现故障,在C处等待救援,B,C之间的距离为10海里,救援船从港口A出发20分钟到达C处,求救援的艇的航行速度.(sin37°≈0.6,cos37°≈0.8, ![]() ≈1.732,结果取整数)
≈1.732,结果取整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】邻边不相等的平行四边形纸片,剪去一个菱形,余下的一个四边形,称为第一次操作;在余下的四边形纸片中再剪去一个菱形,又余下一个四边形,称为第二次操作;…依此类推,若第n次操作余下的四边形是菱形,则称原平行四边形为n阶准菱形,如图1,ABCD中,若AB=1,BC=2,则ABCD为1阶准菱形.
(1)猜想与计算:
邻边长分别为3和5的平行四边形是阶准菱形;已知ABCD的邻边长分别为a,b(a>b),满足a=8b+r,b=5r,请写出ABCD是阶准菱形.
(2)操作与推理:
小明为了剪去一个菱形,进行了如下操作:如图2,把ABCD沿BE折叠(点E在AD上),使点A落在BC边上的点F处,得到四边形ABFE.请证明四边形ABFE是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=﹣ ![]() x+1的图象与x轴、y轴分别交于点A、B,以线段AB为边在第一象限作等边△ABC.
x+1的图象与x轴、y轴分别交于点A、B,以线段AB为边在第一象限作等边△ABC.
(1)若点C在反比例函数y= ![]() 的图象上,求该反比例函数的解析式;
的图象上,求该反比例函数的解析式;
(2)点P(2 ![]() ,m)在第一象限,过点P作x轴的垂线,垂足为D,当△PAD与△OAB相似时,P点是否在(1)中反比例函数图象上?如果在,求出P点坐标;如果不在,请加以说明.
,m)在第一象限,过点P作x轴的垂线,垂足为D,当△PAD与△OAB相似时,P点是否在(1)中反比例函数图象上?如果在,求出P点坐标;如果不在,请加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】星期天,小明和小芳从同一小区门口同时出发,沿同一路线去离该小区1800米的少年宫参加活动,为响应“节能环保,绿色出行”的号召,两人都步行,已知小明的速度是小芳的速度的1.2倍,结果小明比小芳早6分钟到达,求小芳的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图示,若△ABC内一点P满足∠PAC=∠PBA=∠PCB,则点P为△ABC的布洛卡点.三角形的布洛卡点(Brocard point)是法国数学家和数学教育家克洛尔(A.L.Crelle 1780﹣1855)于1816年首次发现,但他的发现并未被当时的人们所注意,1875年,布洛卡点被一个数学爱好者法国军官布洛卡(Brocard 1845﹣1922)重新发现,并用他的名字命名.问题:已知在等腰直角三角形DEF中,∠EDF=90°,若点Q为△DEF的布洛卡点,DQ=1,则EQ+FQ=( ) 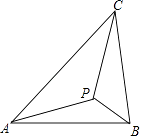
A.5
B.4
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P,Q是反比例函数y= ![]() 图象上的两点,PA⊥y轴于点A,QN⊥x轴于点N,作PM⊥x轴于点M,QB⊥y轴于点B,连接PB、QM,△ABP的面积记为S1 , △QMN的面积记为S2 , 则S1S2 . (填“>”或“<”或“=”)
图象上的两点,PA⊥y轴于点A,QN⊥x轴于点N,作PM⊥x轴于点M,QB⊥y轴于点B,连接PB、QM,△ABP的面积记为S1 , △QMN的面积记为S2 , 则S1S2 . (填“>”或“<”或“=”) 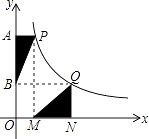
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com