
【题目】如图,在平面直角坐标系中,点A(m,n)(m>0)在双曲线y=![]() 上.
上.
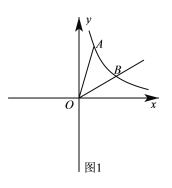
(1)如图1,m=1,∠AOB=45°,点B正好在y=![]() (x>0)上,求B点坐标;
(x>0)上,求B点坐标;
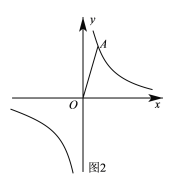
(2)如图2,线段OA绕O点旋转至OC,且C点正好落在y=![]() 上,C(a,b),试求m与a的数量关系.
上,C(a,b),试求m与a的数量关系.
【答案】(1)B(![]() ,
,![]() );(2)
);(2)![]() 或
或![]() ,
,![]()
【解析】
(1)作出辅助线如图,证得Rt△FAO![]() Rt△DAG,求得点G的坐标为(5,3),继而求得直线OG的解析式,从而求得点B的坐标;
Rt△DAG,求得点G的坐标为(5,3),继而求得直线OG的解析式,从而求得点B的坐标;
(2)由题意得A(m,![]() ),C(a,
),C(a,![]() ),OA2=OC2,计算整理得(m2-a2)(1-
),OA2=OC2,计算整理得(m2-a2)(1-![]() )=0,即可求解.
)=0,即可求解.
(1)∵点A(m,n)在双曲线y=![]() 上,且m=1,
上,且m=1,
∴![]() ,
,
∴点A的坐标为(1,4),
作AG⊥OA交直线OB于点G,作GE⊥y轴于E,作AF⊥y轴于F,作AD⊥![]() 轴交GE于点D,如图所示:
轴交GE于点D,如图所示:
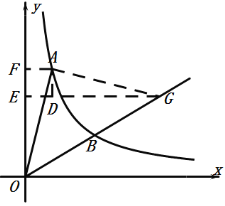
∵点A的坐标为(1,4),
∴FA=1,FO=4,
∵AG⊥OA,∠AOB=45°,
∴△AOG为等腰直角三角形,
∴AO=AG,
∵∠FAO+∠OAD=∠DAG+∠OAD=90°,
∴∠FAO=∠DAG,
∴Rt△FAO![]() Rt△DAG,
Rt△DAG,
∴FO= DG=4,FA=DA=1,
∵GE⊥y轴, AF⊥y轴,AD⊥![]() 轴,FA=DA=1,
轴,FA=DA=1,
∴四边形ADEF为正方形,
∴FA=DA= DE=EF=1,
∴GE=DE+DG=5,EO=FO-EF=3,
∴点G的坐标为(5,3),
设直线OG的解析式为![]() ,
,
把点G的坐标为(5,3)代入得:![]() ,
,
∴直线OG的解析式为![]() ,
,
解方程组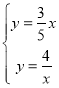 ,
,
得: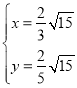 (负值已舍),
(负值已舍),
∴点B的坐标为(![]() ,
,![]() );
);
(2)根据题意:A(m,![]() ),C(a,
),C(a,![]() ),
),
∵OA2=OC2,
∴m2+![]() =
=![]() 2+
2+![]() ,
,
整理得:(m2-a2)(1-![]() )=0,(
)=0,(![]() )(
)(![]() )(
)(![]() )(
)(![]() )=0,
)=0,
∵![]() ,
,
∴![]() 或
或![]() ,
,![]() .
.


 作业辅导系列答案
作业辅导系列答案科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,D、E分别在边AB、AC上,下列条件中,不能确定△ADE∽△ACB的是( )
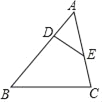
A. ∠AED=∠B B. ∠BDE+∠C=180°
C. ADBC=ACDE D. ADAB=AEAC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了落实国务院的指示精神,某地方政府出台了一系列“三农”优惠政策,使农民收入大幅度增加.某农户生产经销一种农产品,已知这种产品的成本价为每千克20元,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系:y=﹣2x+80.设这种产品每天的销售利润为w元.
(1)求w与x之间的函数关系式.
(2)该产品销售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种产品的销售价不高于每千克28元,该农户想要每天获得150元的销售利润,销售价应定为每千克多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若抛物线![]() 与
与![]() 轴相交于
轴相交于![]() ,
,![]() 两点,与
两点,与![]() 轴相交于点
轴相交于点![]() ,直线
,直线![]() 经过点
经过点![]() ,
,![]() .
.
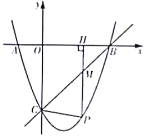
(1)求抛物线的解析式;
(2)点![]() 是直线
是直线![]() 下方抛物线上一动点,过点
下方抛物线上一动点,过点![]() 作
作![]() 轴于点
轴于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.
①线段![]() 是否有最大值?如果有,求出最大值;如果没有,请说明理由;
是否有最大值?如果有,求出最大值;如果没有,请说明理由;
②在点![]() 运动的过程中,是否存在点
运动的过程中,是否存在点![]() ,恰好使
,恰好使![]() 是以
是以![]() 为腰的等腰三角形?如果存在,请直接写出点
为腰的等腰三角形?如果存在,请直接写出点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
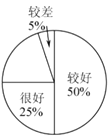
【题目】我国北方又进入了火灾多发季节,为此,某校在全校1200名学生中随机抽取一部分人进行“安全防火,警钟长鸣”知识问卷调查活动,对问卷调查成绩按“很好”、“较好”、“一般”“较差”四类汇总分析,并绘制了如下扇形统计图和条形统计图.
(1)本次活动共抽取了多少名同学?
(2)补全条形统计图;
(3)根据以上调查结果分析,估计该校1200名学生中,对“安全防火”知识了解“较好”和“很好”的学生大约共计有多少名.
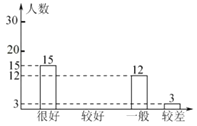
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=![]() AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①∠AED=∠CED;②OE=OD;③BH=HF;④BC﹣CF=2HE;⑤AB=HF,其中正确的有( )
AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①∠AED=∠CED;②OE=OD;③BH=HF;④BC﹣CF=2HE;⑤AB=HF,其中正确的有( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
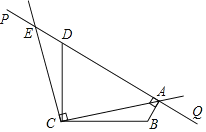
【题目】如图,∠BCD=90°,且BC=DC,直线PQ经过点D.设∠PDC=α(45°<α<135°),BA⊥PQ于点A,将射线CA绕点C按逆时针方向旋转90°,与直线PQ交于点E.
(1)当α=125°时,∠ABC= °;
(2)求证:AC=CE;
(3)若△ABC的外心在其内部,直接写出α的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在ABCD中,DE平分∠ADB,交AB于E,BF平分∠CBD,交CD于F.
(1)求证:△ADE≌△CBF;
(2)当AD与BD满足什么关系时,四边形DEBF是矩形?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com