
【题目】某种产品形状是长方形,长为8cm,它的展开图如图:
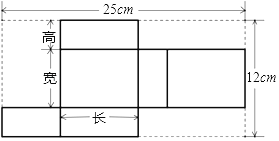
(1)求长方体的体积;
(2)请为厂家设计一种包装纸箱,使每箱能装10件这种产品,要求没有空隙且要使该纸箱所用材料尽可能少(纸箱的表面积尽可能小)
【答案】(1)长方形的体积为144cm3;(2)纸箱的表面积为792cm2
【解析】
(1)设长方体的高为xcm,则长方形的宽为(12﹣2x)cm,根据长方体的展开图可见产品的一个宽+2个长+一个高=25,从而列出方程,求解得出长方体产品的长宽高,再根据长方体的体积计算方法即可算出答案;
(2)由于产品的长宽高是固定的,厂家设计一种包装纸箱,使每箱能装10件这种产品,要求没有空隙且要使该纸箱所用材料尽可能少,故在装这10件产品时,让产品重叠在一起的面积尽可能的大,从而得出设计的包装纸箱为15×12×8规格,再根据长方体的表面积计算方法即可算出答案.
(1)解:设长方体的高为xcm,则长方形的宽为(12﹣2x)cm,根据题意可得:
12﹣2x+8+x+8=25,
解得:x=3,
所以长方体的高为3cm,宽为6cm,长为8cm,
长方形的体积为:8×6×3=144cm3;
(2)解:由要求没有空隙且要使该纸箱所用材料尽可能少(纸箱的表面积尽可能小),可知纸箱的装法有两种,即每层一个共10层或每层两个共5层,
①每层一个共10层:
(ⅰ)当3×6的面叠加在一起时,
表面积为2(3×6+3×80+6×80)=1476cm2,
(ⅱ)当3×8的面叠加在一起时,
表面积为2(3×8+3×60+8×60)=1368cm2,
(ⅲ)当6×8的面叠加在一起时,
表面积为2(30×8+30×6+8×6)=936cm2,
②每层两个共5层:
(ⅰ)当每一层的两个长方体的3×6的面叠加在一起时,且底层的长方体的3×8的面贴地面时,
表面积为2(3×16+3×30+16×30)=1236cm2,
(ⅱ)当每一层的两个长方体的3×6的面叠加在一起时,且底层的长方体的6×8的面贴地面时,
表面积为2(6×16+6×15+16×15)=852cm2,
(ⅲ)当每一层的两个长方体的3×8的面叠加在一起时,且底层的长方体的3×6的面贴地面时,
表面积为2(3×12+3×40+12×40)=1272cm2,
(ⅳ)当每一层的两个长方体的3×8的面叠加在一起时,且底层的长方体的8×6的面贴地面时,
表面积为2(12×8+8×15+12×15)=792cm2,
(ⅴ)当每一层的两个长方体的8×6的面叠加在一起时,且底层的长方体的8×3的面贴地面时,
表面积为2(6×8+6×30+8×30)=936cm2,
(ⅵ)当每一层的两个长方体的8×6的面叠加在一起时,且底层的长方体的6×3的面贴地面时,
表面积为2(6×6+6×40+6×40)=1032cm2,
所以当每一层的两个长方体的3×8的面叠加在一起时,且底层的长方体的8×6的面贴地面时,表面积最小,为792cm2,设计的包装纸箱为长为12cm,宽为8cm,高为15cm.
故答案为:792cm2


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:
【题目】阅读理解:
若A、B、C为数轴上三点,若点C到A的距离是点C到B的距离2倍,我们就称点C是【A,B】的好点.
如图1,点A表示的数为﹣1,点B表示的数为2.表示1的点C到点A的距离是2,到点B的距离是1,那么点C是【A,B】的好点.
知识运用:
(1)如图1,表示0的点D到点A的距离是1,到点B的距离是2,那么点D 【A,B】的好点;(请在横线上填是或不是)
(2)如图2,M、N为数轴上两点,点M所表示的数为4,点N所表示的数为﹣2.数 所对应的点是【M,N】的好点(写出所有可能的情况);
拓展提升:
(3)如图3,A、B为数轴上两点,点A所表示的数为﹣20,点B所表示的数为40.现有一只电子蚂蚁P从点B出发,以4个单位每秒的速度向左运动,到达点A停止.当经过几秒时,P、A和B中恰有一个点为其余两点的好点?(写出所有情况)
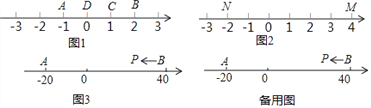
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个由5张纸片拼成的平行四边形,相邻纸片之间互不重叠也无缝隙,其中两张等腰直角三角形纸片的面积都为S1 , 另两张直角三角形纸片的面积都为S2 , 中间一张正方形纸片的面积为S3 , 则这个平行四边形的面积一定可以表示为( )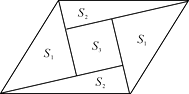
A.4S1
B.4S2
C.4S2+S3
D.3S1+4S3
查看答案和解析>>
科目:初中数学 来源: 题型:
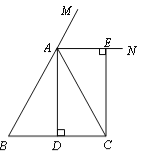
【题目】(10分)已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,猜想四边形ADCE的形状,并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,矩形OABC的顶点A在x轴上,顶点C在y轴上,B(4,3),连接OB,将△OAB沿直线OB翻折,得△ODB,OD与BC相交于点E,若双曲线 ![]() 经过点E,则k= ;
经过点E,则k= ;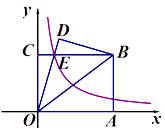
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△AOB中,A(-8,0),B(0, ![]() ),AC平分∠OAB,交y轴于点C,点P是x轴上一点,⊙P经过点A、C,与x轴于点D,过点C作CE⊥AB,垂足为E,EC的延长线交x轴于点F,
),AC平分∠OAB,交y轴于点C,点P是x轴上一点,⊙P经过点A、C,与x轴于点D,过点C作CE⊥AB,垂足为E,EC的延长线交x轴于点F,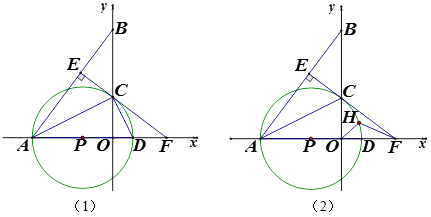
(1)求⊙P的半径;
(2)求证:EF为⊙P的切线;
(3)若点H是 ![]() 上一动点,连接OH、FH,当点P在
上一动点,连接OH、FH,当点P在 ![]() 上运动时,试探究
上运动时,试探究 ![]() 是否为定值?若为定值,求其值;若不是定值,请说明理由.
是否为定值?若为定值,求其值;若不是定值,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年11月读书节,深圳市统计某学校九年级学生读书状况,制作了两幅不完整的统计图如图所示.
(1)x的值为 ,参加调查的总人数为 人;
(2)补全条形统计图;
(3)若全市有6.7万学生,则看3本及3本书以上的学生约有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数中y=ax2+bx﹣3的x、y满足表:
x | … | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | 0 | ﹣3 | ﹣4 | ﹣3 | m | … |
(1)求该二次函数的解析式;
(2)求m的值并直接写出对称轴及顶点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB、CD分别表示两幢相距36米的大楼,高兴同学站在CD大楼的P处窗口观察AB大楼的底部B点的俯角为45°,观察AB大楼的顶部A点的仰角为30°,求大楼AB的高. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com