
【题目】用适当方法解下列方程:
①x2﹣2x=99
②x2+8x=﹣16
③x2+3x+1=0
④5x(x+2)=4x+8.
【答案】①x1=11,x2=﹣9;②x1=x2=﹣4;③x1=![]() ,x2=
,x2=![]() ;④x1=﹣2,x2=
;④x1=﹣2,x2=![]() .
.
【解析】
】①移项后分解因式,即可得出两个一元一次方程,求出方程的解即可;
②移项后分解因式,即可得出两个一元一次方程,求出方程的解即可;
③求出b2-4ac的值,再代入公式求出即可;
④移项后分解因式,即可得出两个一元一次方程,求出方程的解即可.
解:①x2﹣2x=99,
x2﹣2x﹣99=0,
(x﹣11)(x+9)=0,
x﹣11=0,x+9=0,
x1=11,x2=﹣9;
②x2+8x=﹣16,
x2+8x+16=0,
(x+4)2=0,
x+4=0,
x=﹣4,
即x1=x2=﹣4;
③x2+3x+1=0,
b2﹣4ac=32﹣4×1×1=5,
x=![]() ,
,
x1=![]() ,x2=
,x2=![]() ;
;
④5x(x+2)=4x+8
5x(x+2)﹣4(x+2)=0,
(x+2)(5x﹣4)=0,
x+2=0,5x﹣4=0,
x1=﹣2,x2=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】“绿水青山就是金山银山”,为保护生态环境,A,B两村准备各自清理所属区域养鱼网箱和捕鱼网箱,每村参加清理人数及总开支如下表:
村庄 | 清理养鱼网箱人数/人 | 清理捕鱼网箱人数/人 | 总支出/元 |
A | 15 | 9 | 57000 |
B | 10 | 16 | 68000 |
(1)若两村清理同类渔具的人均支出费用一样,求清理养鱼网箱和捕鱼网箱的人均支出费用各是多少元;
(2)在人均支出费用不变的情况下,为节约开支,两村准备抽调40人共同清理养鱼网箱和捕鱼网箱,要使总支出不超过102000元,且清理养鱼网箱人数小于清理捕鱼网箱人数,则有哪几种分配清理人员方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知点A(0,2),B(2,2),抛物线F:y=x2﹣2mx+m2﹣2.

(1)求抛物线F的顶点坐标(用含m的式子表示);
(2)当抛物线F与线段AB有公共点时,直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在菱形ABCD中,动点P从点B出发,沿折线B→C→D→B运动.设点P经过的路程为x,△ABP的面积为y.把y看作x的函数,函数的图象如图②所示,则图②中的b等于( )
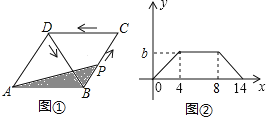
A. ![]() B.
B. ![]() C. 5D. 4
C. 5D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有大小两种货车,3辆大货车与4辆小货车一次可以运货18吨,2辆大货车与6辆小货车一次可以运货17吨.
(1)请问1辆大货车和1辆小货车一次可以分别运货多少吨?
(2)目前有33吨货物需要运输,货运公司拟安排大小货车共计10辆,全部货物一次运完,其中每辆大货车一次运费花费130元,每辆小货车一次运货花费100元,请问货运公司应如何安排车辆最节省费用?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某集团公司为适应市场竞争,赶超世界先进水平,每年将销售总额的8%作为新产品开发研究资金,该集团2000年投入新产品开发研究资金为4000万元,2002年销售总额为7.2亿元,求该集团2000年到2002年的年销售总额的平均增长率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,M、N是边长为6的正方形ABCD的边CD上的两个动点,满足AM=BN,连接AC交BN于点E,连接DE交AM于点F,连接CF.
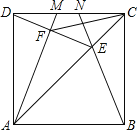
(1)求证:DE=BE;
(2)判断DE与AM的位置关系,并证明;
(3)判断线段CF是否存在最小值?若存在,求出来,若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB=60°,半径为2![]() 的⊙M与边OA、OB相切,若将⊙M水平向左平移,当⊙M与边OA相交时,设交点为E和F,且EF=6,则平移的距离为( )
的⊙M与边OA、OB相切,若将⊙M水平向左平移,当⊙M与边OA相交时,设交点为E和F,且EF=6,则平移的距离为( )

A. 2 B. 2或6 C. 4或6 D. 1或5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com