
【题目】如图,M、N是边长为6的正方形ABCD的边CD上的两个动点,满足AM=BN,连接AC交BN于点E,连接DE交AM于点F,连接CF.
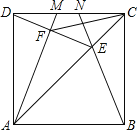
(1)求证:DE=BE;
(2)判断DE与AM的位置关系,并证明;
(3)判断线段CF是否存在最小值?若存在,求出来,若不存在,说明理由.
【答案】(1)见解析;(2)DE⊥AM,见解析;(3)存在最小值,最小值为![]() .
.
【解析】
(1)证明△DAE≌△BAE(SAS)即可解决问题.
(2)想办法证明∠DAM=∠EDC即可.
(3)存在最小值.如图,取AD的中点O,连接OF、OC,利用三角形三边关系解决问题即可.
解:(1)证明:在正方形ABCD中,AD=AB,∠DAE=BAE,又AE为公共边,
∴△DAE≌△BAE(SAS),
∴DE=BE.
(2)结论:互相垂直.
理由::在正方形ABCD中,AD=BC=CD,∠ADC=∠BCD=90°,
∵AM=BN,
∴Rt△ADM≌Rt△BCN(HL),
∴∠DAM=∠CBN
由(1)知DE=BE,又CD=CB,CE为公共边,
∴△DCE≌△BCE(SSS),
∴∠CDE=∠CBE
∵∠ADF+∠CDE=∠ADC=90°
∴∠DAF+∠ADF=90°
∴∠DFA=180°﹣90°=90°
即DE⊥AM.
(3)存在最小值.如图,取AD的中点O,连接OF、OC,
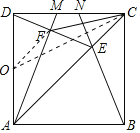
则OF=DO=![]() AD=3,
AD=3,
在Rt△OCD中,
OC=![]() ,
,
根据三角形的三边关系,OF+CF>OC,
∴当O、F、C三点共线时,CF的长度最小,最小值为OC﹣OF=![]() .
.


科目:初中数学 来源: 题型:
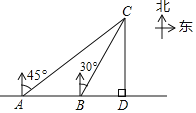
【题目】今年“五一”期间,小明一家到某农庄采摘,在村口A处,小明接到农庄发来的定位,发现农庄C在自己的北偏东45°方向,于是沿河边笔直绿道l步行200米到达B处,此时定位显示农庄C在自己的北偏东30°方向,电话联系,得知农庄主已到农庄C正南方的桥头D处等待,请问还要沿绿道直走多少米才能到达桥头D处.(精确到1米,参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
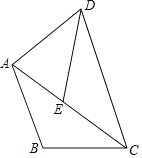
【题目】如图,将△ABC绕点C顺时针旋转36°,点B的对应点为点E,点A的对应点为点D,此时点E恰好落在边AC上时,连接AD,若AB=BC,AC=2,则AB的长度是( )
A. ![]() B. 1C.
B. 1C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图分别是五角星、六角星、七角星、八角星的图形;
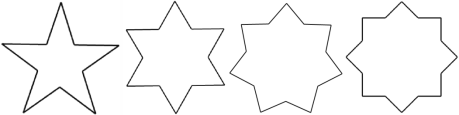
(1)请问其中是中心对称图形的是哪些?
(2)依次类推,36角星是不是中心对称图形?
(3)怎样判断一个n角星是否是中心对称图形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场服装部为了解服装的销售情况,统计了每位营业员在某月的销售额(单位:万元),并根据统计的这组销售额数据,绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
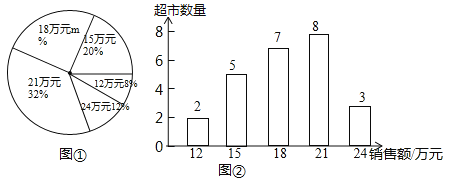
(Ⅰ)该商场服装部营业员的人数为_____________,图①中![]() 的值为____________;
的值为____________;
(Ⅱ)求统计的这组销售额数据的平均数、众数和中位数.
查看答案和解析>>
科目:初中数学 来源: 题型:
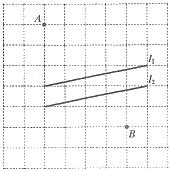
【题目】如图,在每个小正方形的边长为1的网格中,点![]() 均在格点上,
均在格点上,![]() 是一条小河平行的两岸.
是一条小河平行的两岸.
(Ⅰ)![]() 的距离等于_____;
的距离等于_____;
(Ⅱ)现要在小河上修一座垂直于两岸的桥![]() (点
(点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,桥的宽度忽略),使
上,桥的宽度忽略),使![]() 最短,请在如图所示的网格中,用无刻度的直尺,画出
最短,请在如图所示的网格中,用无刻度的直尺,画出![]() ,并简要说明点
,并简要说明点![]() ,
,![]() 的位置是如何找到的(不要求证明)_________________________________.
的位置是如何找到的(不要求证明)_________________________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com