
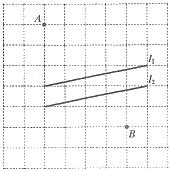
【题目】如图,在每个小正方形的边长为1的网格中,点![]() 均在格点上,
均在格点上,![]() 是一条小河平行的两岸.
是一条小河平行的两岸.
(Ⅰ)![]() 的距离等于_____;
的距离等于_____;
(Ⅱ)现要在小河上修一座垂直于两岸的桥![]() (点
(点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,桥的宽度忽略),使
上,桥的宽度忽略),使![]() 最短,请在如图所示的网格中,用无刻度的直尺,画出
最短,请在如图所示的网格中,用无刻度的直尺,画出![]() ,并简要说明点
,并简要说明点![]() ,
,![]() 的位置是如何找到的(不要求证明)_________________________________.
的位置是如何找到的(不要求证明)_________________________________.
【答案】![]() 取格点
取格点![]() ,连接
,连接![]() ,(使
,(使![]() ),取格点
),取格点![]() 、
、![]() ,连接
,连接![]() (使
(使![]() ),与
),与![]() 交于点
交于点![]() ;同理作点
;同理作点![]() ;连接
;连接![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() ,即为所求
,即为所求
【解析】
(Ⅰ)利用勾股定理求出AB的长即可;(Ⅱ)要使![]() 最短,则MN⊥l1,AM与BN转化成一条线段时最短,取格点
最短,则MN⊥l1,AM与BN转化成一条线段时最短,取格点![]() ,连接
,连接![]() ,交l1于Q,交l2于P,由网格性质可得AC⊥l1,由l1//l2可得平行线间的距离PQ=MN的长,取格点
,交l1于Q,交l2于P,由网格性质可得AC⊥l1,由l1//l2可得平行线间的距离PQ=MN的长,取格点![]() 、
、![]() ,连接
,连接![]() ,交AC于A′,根据相似三角形的性质可得AA′=PQ,同理可作点B′,则BB′=PQ,连接
,交AC于A′,根据相似三角形的性质可得AA′=PQ,同理可作点B′,则BB′=PQ,连接![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() 与
与![]() 交于点
交于点![]() ,则BB′=PQ,可得四边形AA′BB′是平行四边形,由全等三角形的性质可得AM=A′N,可得四边形AA′MN是平行四边形,可知MN⊥l1,同理BN=B′M,则AM+BN=AB′距离最短,即可得解.
,则BB′=PQ,可得四边形AA′BB′是平行四边形,由全等三角形的性质可得AM=A′N,可得四边形AA′MN是平行四边形,可知MN⊥l1,同理BN=B′M,则AM+BN=AB′距离最短,即可得解.
(Ⅰ)AB=![]() =
=![]() .
.
故答案为:![]()
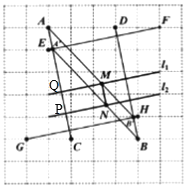
(Ⅱ)如图,取格点![]() ,连接
,连接![]() ,(使
,(使![]() ),交l1于Q,交l2于P,
),交l1于Q,交l2于P,
∴PQ⊥l1,
∴PQ=![]() ,
,
取格点![]() 、
、![]() ,连接
,连接![]() (使
(使![]() ),与
),与![]() 交于点
交于点![]() ;
;
∵∠AFE=∠EAA′,∠AEF=∠AEF,
∴△AA′E∽△FAE,
∴![]() ,
,
∴AA′=![]() ,
,
∴AA′=PQ,
同理作点![]() ;连接
;连接![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() ,
,
∴BB′=AA′=PQ,
∵BB′//AA′,
∴四边形AA′BB′,
∴AB′//A′B,
∴∠QAM=∠PA′N,
又∵AQ=A′P,∠AQM=∠A′PN,
∴△AQM≌△A′PN,
∴AM=A′N,
∴四边形AA′MN是平行四边形,
∴AA′//MN,
∴MN⊥l1,
同理:BN=B′M,
∴AM+BN=AB′距离最短,
∴![]() 即为所求.
即为所求.
故答案为:取格点![]() ,连接
,连接![]() ,(使
,(使![]() ),取格点
),取格点![]() 、
、![]() ,连接
,连接![]() (使
(使![]() ),与
),与![]() 交于点
交于点![]() ;同理作点
;同理作点![]() ;连接
;连接![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() ,即为所求
,即为所求


科目:初中数学 来源: 题型:
【题目】如图,M、N是边长为6的正方形ABCD的边CD上的两个动点,满足AM=BN,连接AC交BN于点E,连接DE交AM于点F,连接CF.
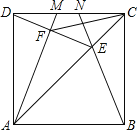
(1)求证:DE=BE;
(2)判断DE与AM的位置关系,并证明;
(3)判断线段CF是否存在最小值?若存在,求出来,若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB=60°,半径为2![]() 的⊙M与边OA、OB相切,若将⊙M水平向左平移,当⊙M与边OA相交时,设交点为E和F,且EF=6,则平移的距离为( )
的⊙M与边OA、OB相切,若将⊙M水平向左平移,当⊙M与边OA相交时,设交点为E和F,且EF=6,则平移的距离为( )

A. 2 B. 2或6 C. 4或6 D. 1或5
查看答案和解析>>
科目:初中数学 来源: 题型:
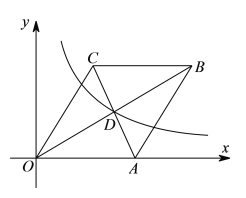
【题目】如图,在平面直角坐标系中,菱形![]() 的边
的边![]() 在
在![]() 轴上,
轴上,![]() 与
与![]() 交于点
交于点![]() ,反比例函数
,反比例函数![]() 的图象经过点
的图象经过点![]() .若将菱形
.若将菱形![]() 向左平移
向左平移![]() 个单位,使点
个单位,使点![]() 落在该反比例函数图象上,则
落在该反比例函数图象上,则![]() 的值为__________.
的值为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】铁岭“荷花节”举办了为期15天的“荷花美食”厨艺秀.小张购进一批食材制作特色美食,每盒售价为50元,由于食材需要冷藏保存,导致成本逐日增加,第x天(1≤x≤15且x为整数)时每盒成本为p元,已知p与x之间满足一次函数关系;第3天时,每盒成本为21元;第7天时,每盒成本为25元,每天的销售量为y盒,y与x之间的关系如下表所示:
第x天 | 1≤x≤6 | 6<x≤15 |
每天的销售量y/盒 | 10 | x+6 |
(1)求p与x的函数关系式;
(2)若每天的销售利润为w元,求w与x的函数关系式,并求出第几天时当天的销售利润最大,最大销售利润是多少元?
(3)在“荷花美食”厨艺秀期间,共有多少天小张每天的销售利润不低于325元?请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进A,B两种型号的手机,已知每部A型号手机的进价比每部B型号手机进价多500元,每部A型号手机的售价是2500元,每部B型号手机的售价是2100元.
(1)若商场用50000元共购进A型号手机10部,B型号手机20部,求A、B两种型号的手机每部进价各是多少元?
(2)为了满足市场需求,商场决定用不超过7.5万元采购A、B两种型号的手机共40部,且A型号手机的数量不少于B型号手机数量的2倍.
①该商场有哪几种进货方式?
②该商场选择哪种进货方式,获得的利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
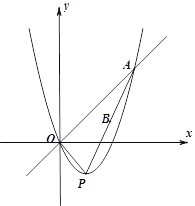
【题目】如图,已知直线![]() 与二次函数
与二次函数![]() 的图像交于点A、O,(O是坐标原点),点P为二次函数图像的顶点,OA=
的图像交于点A、O,(O是坐标原点),点P为二次函数图像的顶点,OA=![]() ,AP的中点为B.
,AP的中点为B.
(1)求二次函数的解析式;
(2)求线段OB的长;
(3)若射线OB上存在点Q,使得△AOQ与△AOP相似,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农场要建一个长方形的养鸡场,鸡场的一边靠长为18m的墙,另三边用木栏围城,木栏长为32m.

(1)鸡场的面积能围成120m2吗?
(2)鸡场的面积能围成130m2吗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com