
分析 (1)将t的值代入“再生二次函数”中,通过配方可得到顶点的坐标;
(2)将点A的坐标代入抛物线E上直接进行验证即可;
(3)已知点B在抛物线E上,将该点坐标代入抛物线E的解析式中直接求解,即可得到n的值.
【发现】
将抛物线l展开,然后将含t值的式子整合到一起,令该式子为0(此时无论t取何值都不会对函数值产生影响),即可求出这个定点的坐标.
【应用1】
将【发现】中得到的两个定点坐标代入二次函数y=-3x2+5x+2中进行验证即可
【应用2】设抛物线E截x轴的线段长为a,先利用三角形的面积求出a的长,再根据点A的坐标求出与x轴的另一交点的坐标,然后代入抛物线求解即可得到t的值,从而得解.
解答 解:【尝试】
(1)∵将t=2代入抛物线l中,得:y=t(x2-3x+2)+(1-t)(-2x+4)=2x2-4x=2(x-1)2-2,
∴此时抛物线的顶点坐标为:(1,-2),
故答案为:(1,-2);
(2)∵将x=2代入y=t(x2-3x+2)+(1-t)(-2x+4),得 y=0,
∴点A(2,0)在抛物线l上,
故答案为:是;
(3)将x=-1代入抛物线l的解析式中,得:
n=t(x2-3x+2)+(1-t)(-2x+4)=6,
故答案为:6;
【发现】
∵将抛物线E的解析式展开,得:
y=t(x2-3x+2)+(1-t)(-2x+4)=t(x-2)(x+1)-2x+4,
∴抛物线l必过定点(2,0)、(-1,6),
故答案为:(2,0)、(-1,6);
【应用一】
将x=2代入y=-3x2+5x+2,y=0,即点A在抛物线上.
将x=-1代入y=-3x2+5x+2,计算得:y=-6≠6,
即可得抛物线y=-3x2+5x+2不经过点B,
二次函数y=-3x2+5x+2不是二次函数y=x2-3x+2和一次函数y=-2x+4的一个“再生二次函数;
【应用二】
由(1)得,抛物线E与x轴的一个交点为A(2,0),点B的坐标为(-1,6),
设抛物线E截x轴的线段长为a,则S=$\frac{1}{2}$a×6=6,
解得a=2,所以,与x轴的另一个交点为C(0,0)或(4,0),
当C点坐标为(0,0)时,yE=2x2-4x;
当C点坐标为(4,0)时,yE=x2-$\frac{12}{5}$x+$\frac{16}{5}$.
点评 本题考查了二次函数综合题型,主要利用了联立两函数解析式求交点坐标,验证点是否在二次函数图象上,三角形的面积,二次函数图象上点的坐标特征,读懂题目信息,理解“再生二次函数”的定义是解题的关键.


科目:初中数学 来源: 题型:填空题
 北京紫禁城是中国古代汉族宫廷建筑之精华.经测算发现,太和殿,中和殿,保和殿这三大殿的矩形宫院ABCD(北至保和殿,南至太和门,西至弘义阁,东至体仁阁)与三大殿下的工字形大台基所在的矩形区域EFGH为相似形.若比较宫院与台基之间的比例关系,可以发现接近于9:5,取“九五至尊”之意.根据测量数据,三大殿台基的宽为40丈,请你估算三大殿宫院的宽为72丈.
北京紫禁城是中国古代汉族宫廷建筑之精华.经测算发现,太和殿,中和殿,保和殿这三大殿的矩形宫院ABCD(北至保和殿,南至太和门,西至弘义阁,东至体仁阁)与三大殿下的工字形大台基所在的矩形区域EFGH为相似形.若比较宫院与台基之间的比例关系,可以发现接近于9:5,取“九五至尊”之意.根据测量数据,三大殿台基的宽为40丈,请你估算三大殿宫院的宽为72丈.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
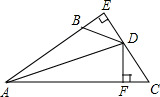 如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,BE=CF,则下列结论:①DE=DF;②AD平分∠BAC;③AE=AD;④AB+AC=2AE中正确的是①②④.
如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,BE=CF,则下列结论:①DE=DF;②AD平分∠BAC;③AE=AD;④AB+AC=2AE中正确的是①②④.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com