
【题目】如图,直线y=![]() x与双曲线y=
x与双曲线y=![]() (k>0,x>0)交于点A,将直线y=
(k>0,x>0)交于点A,将直线y=![]() x向上平移4个单位长度后,与y轴交于点C,与双曲线y=
x向上平移4个单位长度后,与y轴交于点C,与双曲线y=![]() (k>0,x>0)交于点B,若OA=3BC,则k的值为( )
(k>0,x>0)交于点B,若OA=3BC,则k的值为( )

A. 3 B. 6 C. ![]() D.
D. ![]()
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】红旗镇镇政府大力发动农户扩大柑橘和蔬菜种植面积,取得了较好的经济效益.今年红旗镇柑橘和蔬菜的收成比去年一共增加了80吨,其中柑橘的收成比去年增加了20%,蔬菜的收成比去年增加了30%,从而使今年的收成共达到420吨.
(1)红旗镇去年柑橘和蔬菜的收成各多少吨?
(2)由于今年大丰收,红旗镇政府计划用甲、乙两种货车共33辆将柑橘和蔬菜全部一次性运到外地去销售.已知一辆甲种货车最多可装13吨柑橘和3吨蔬菜;一辆乙种货车最多可装柑橘和蔬菜各6吨,安排甲、乙两种货车共有几种方案?
(3)若甲种货车的运费为每辆600元,乙种货车的运费为每辆500元,在(2)的情况下,如何安排运费最少,最少为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】养牛场原有大牛30头和小牛15头,一天约用饲料675kg.一周后又购进12头大牛和5头小牛,这时1天约用饲料940kg.饲养员李大叔估计每头大牛1天约需饲料1820kg,每头小牛1天约需饲料78kg,你能通过计算检验他的估计吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠BAC=90°,点D为线段BC上的一个动点,以AD为直角边向右作等腰Rt△ADF,使AD=AF,∠DAF=90°.
(1)如图1,连结CF,求证:△ABD≌△ACF;
(2)如图2,过A点作△ADF的对称轴交BC于点E,猜想BD2,DE2,CE2关系,并证明你的结论;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠AEF,FH平分∠EFD.求证:EG∥FH.

请完成以下证明过程:
证明:∵AB∥CD(已知)
∴∠AEF=∠EFD(__________________)
∵EG平分∠AEF,FH平分∠EFD(__________)
∴∠___=![]() ∠AEF,∠___=
∠AEF,∠___= ![]() ∠EFD(____________)
∠EFD(____________)
∴∠_____=∠______(等量代换)
∴EG∥FH(__________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】兴隆商场用36万元购进A、B两种品牌的服装,销售完后共获利6万元,其进价和售价如下表:

该商场购进A、B两种服装各多少件?
(2)第二次以原价购进A、B两种服装,购进B服装的件数不变,购进A服装的件数是第一次的2倍,A种服装按原价出售,而B种服装打折销售;若两种服装销售完毕,要使第二次销售活动获利不少于81600元,则B种服装最低打几折销售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】湖南广益实验中学星沙校区将在今年8月份按时开学迎新,据报道该校区投资达6亿元人民币,现在进行紧张有序的施工阶段,届时将成为全国硬件设施最先进的中学校园之一,在之前的建设过程中,某渣土运输公司承担了星沙校区的土方运输任务,拟派出大、小两种型号的渣土车运输土方,已知2辆大型渣土运输车与3辆小型渣土运输车一次共运输土方36吨,5辆大型渣土运输车与7辆小型渣土运输车一次共运输土方87吨.
(1)一辆大型渣土运输车和一辆小型渣土运输车一次各运输土方多少吨?
(2)该渣土运输公司决定派出大、小两种型号渣土运输车共20辆参与运输土方,若每次运输土方总量不小于156吨,且小型渣土运输车至少派出6辆,则有哪几种派车方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
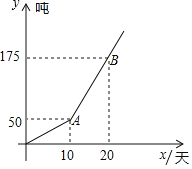
【题目】荔枝是广西盛产的一种水果,六月份是荔技传统销售旺季![]() 去年六月份某水果公司为拓展销售渠道,在实体店的基础上中途增设了网店,公司总销售量
去年六月份某水果公司为拓展销售渠道,在实体店的基础上中途增设了网店,公司总销售量![]() 吨
吨![]() 与销售时间
与销售时间![]() 天
天![]() 关系如图所示:
关系如图所示:
![]() 请直接写出去年六月份网店每天的销售量,并求出AB的解析式
请直接写出去年六月份网店每天的销售量,并求出AB的解析式![]() 不写取值范围
不写取值范围![]() ;
;
![]() 公司预计,今年六月份实体店的销售量与去年相同,网店的销售量将有所增加,预计今年网店每天的销售量比去年增加
公司预计,今年六月份实体店的销售量与去年相同,网店的销售量将有所增加,预计今年网店每天的销售量比去年增加![]() ,公司六月份的总销售量是去年的
,公司六月份的总销售量是去年的![]() 倍,求m的值.
倍,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() 上的图象经过点
上的图象经过点![]() ,直线
,直线![]() 与双曲线
与双曲线![]() 在第二、四象限分别相交于P、Q两点,与x轴、y轴分别相交于C,D两点
在第二、四象限分别相交于P、Q两点,与x轴、y轴分别相交于C,D两点
![]() 求k的值;
求k的值;
![]() 连接OQ,是否存在实数b,使得
连接OQ,是否存在实数b,使得![]() ?若存在,请求出b的值;若不存在,请说明理由.
?若存在,请求出b的值;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com