
【题目】如图,直线![]() 与反比例函数
与反比例函数![]() 在第一象限内的图象交于
在第一象限内的图象交于![]() 、
、![]() 两点,且与
两点,且与![]() 轴的正半轴交于
轴的正半轴交于![]() 点.若
点.若![]() ,
,![]() 的面积为
的面积为![]() ,则
,则![]() 的值为( )
的值为( )

A. 6 B. 9 C. 12 D. 18
【答案】A
【解析】
作AD⊥x轴于D,BE⊥x轴于E,先证明△CBE∽△CAD,利用相似比得到AD=3BE,设B(t,![]() ),利用反比例函数图象上点的坐标特征得到A点坐标为(
),利用反比例函数图象上点的坐标特征得到A点坐标为(![]() t,
t,![]() ),根据反比例函数的比例系数的几何意义得S△AOD=S△BOE,由于S△AOD+S梯形ABED=S△AOB+S△BOE,所以S△AOB=S梯形ABED,然后利用梯形的面积公式计算即可求得.
),根据反比例函数的比例系数的几何意义得S△AOD=S△BOE,由于S△AOD+S梯形ABED=S△AOB+S△BOE,所以S△AOB=S梯形ABED,然后利用梯形的面积公式计算即可求得.
作AD⊥x轴于D,BE⊥x轴于E,如图,
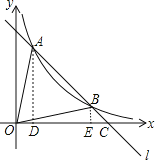
∵BE∥AD,
∴△CBE∽△CAD,
∴![]() =
=![]() ,
,
∵AB=2BC,
∴CB:CA=1:3,
∴![]() =
=![]() =
=![]() ,
,
∴AD=3BE,
设B(t,![]() ),则A点坐标为(
),则A点坐标为(![]() t,
t,![]() ),
),
∵S△AOD+S梯形ABED=S△AOB+S△BOE,
而S△AOD=S△BOE,=![]() k,
k,
∴S△AOB=S梯形ABED=![]() (
(![]() +
+![]() )(t
)(t![]() t)=8,
t)=8,
解得k=6.
故答案选A.


科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:
①BD=CE;②∠ACE+∠DBC=45°;③BD⊥CE;④∠BAE+∠DAC=180°.其中结论正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c与x轴交于点A(-1,0),顶点坐标(1,n)与y轴的交点在(0,2),(0,3)之间(包含端点),则下列结论:①3a+b<0;②-1≤a≤-![]() ;③对于任意实数m,a+b≥am2+bm总成立;④关于x的方程ax2+bx+c=n-1有两个不相等的实数根.其中结论正确的个数为( )
;③对于任意实数m,a+b≥am2+bm总成立;④关于x的方程ax2+bx+c=n-1有两个不相等的实数根.其中结论正确的个数为( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在四边形ABCD中,AB=BC=CD=DA=5 cm,BD=8 cm.则AC= cm;
(2)在宽为8 cm 的长方形纸带上,用图1中的四边形设计如图2所示的图案.
①如果用7个图1中的四边形设计图案,那么至少需要 cm长的纸带;
②设图1中的四边形有x个,所需的纸带长为y cm,求y与x之间的函数表达式;
③在长为40 cm的纸带上,按照这种方法,最多能设计多少个图1中的四边形?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“丰收1号”小麦的试验田是边长为![]() 米(a>1)的正方形减去一个边长为1米的正方形蓄水池后余下的部分,“丰收2号”小麦的试验田是边长为(
米(a>1)的正方形减去一个边长为1米的正方形蓄水池后余下的部分,“丰收2号”小麦的试验田是边长为(![]() )米的正方形,两块试验田里的小麦都收获了500千克.(1)哪种小麦的单位面积产量高?(2)高的单位面积产量是低的单位面积产量的多少倍?
)米的正方形,两块试验田里的小麦都收获了500千克.(1)哪种小麦的单位面积产量高?(2)高的单位面积产量是低的单位面积产量的多少倍?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 与
与![]() 轴负半轴交于点
轴负半轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,![]() (
(![]() 点在
点在![]() 点的右侧),点
点的右侧),点![]() 是抛物线上对称轴上的一动点,且
是抛物线上对称轴上的一动点,且![]() 的面积为
的面积为![]() .
.
(1)求![]() 的值;
的值;
(2)![]() 的面积为
的面积为![]() ,直接写出
,直接写出![]() 点坐标.
点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)某工厂计划在规定时间内生产24000个零件,若每天比原计划多生产30个零件,则在规定时间内可以多生产300个零件.
(1)求原计划每天生产的零件个数和规定的天数.
(2)为了提前完成生产任务,工厂在安排原有工人按原计划正常生产的同时,引进5组机器人生产流水线共同参与零件生产,已知每组机器人生产流水线每天生产零件的个数比20个工人原计划每天生产的零件总数还多20%,按此测算,恰好提前两天完成24000个零件的生产任务,求原计划安排的工人人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,解一元一次方程,可以把它转化为两个一元一次方程来解,其实用“转化”的数学思想,我们还可以解一些新的方程,例如一元三次方程x3+x2﹣2x=0,可以通过因式分解把它转化为x(x2+x﹣2)=0,解方程x=0和x2+x﹣2=0,可得方程x3+x2﹣2x=0的解.
(1)方程x3+x2﹣2x=0的解是x1=0,x2= ,x3= .
(2)用“转化”思想求方程![]() =x的解.
=x的解.
(3)如图,已知矩形草坪ABCD的长AD=14m,宽AB=12m,小华把一根长为28m的绳子的一端固定在点B处,沿草坪边沿BA、AD走到点P处,把长绳PB段拉直并固定在点P处,然后沿草坪边沿PD、DC走到点C处,把长绳剩下的一段拉直,长绳的另一端恰好落在点C处,求AP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象相交于A、B两点,A点坐标是(﹣2,1),B点坐标(1,n);
的图象相交于A、B两点,A点坐标是(﹣2,1),B点坐标(1,n);
(1)求出k,b,m,n的值;
(2)求△AOB的面积;
(3)直接写出一次函数的函数值大于反比例函数的函数值的x的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com