
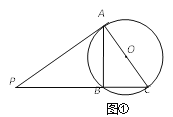
【题目】初步探究
如图①,过点P的两条直线分别与⊙O相切于点A,与⊙O相交于B、C两点,且AC恰好经过圆心O.求证△PAB∽△PCA.
进一步探究
如图②若其他条件不变,但AC不经过圆心O.上述结论是否成立?请说明理由.

尝试应用
如图③,PA=3,PB=![]() ,⊙O的半径为2,请直接写出直线PC上一点与圆心O的最短距离.
,⊙O的半径为2,请直接写出直线PC上一点与圆心O的最短距离.

【答案】(1)证明见解析;(2)成立.理由见解析(3)1.
【解析】试题分析:(1)、根据切线的性质得出∠PAB+∠BAC=90°,根据直径的性质得出∠BAC+∠C=90°,从而得出∠PAB=∠C,结合公共角得出三角形相似;(2)、连接AO,延长AO交⊙O于D,连接BD,然后根据第一题相似的方法得出三角形相似;(3)、当AC为直径时以及三角形相似得出最短距离.
试题解析:(1)∵PA与⊙O相切, ∴∠PAC=90° ∴∠1+∠PAB=90°.
∵AC是⊙O的直径 ∴∠1+∠C=90° ∴∠PAB=∠C 又∵∠P=∠P ∴△PAB∽△PCA
(2)成立.连接AO,延长AO交⊙O于D,连接BD.
∵PA与⊙O相切 ∴∠PAD=90° ∴∠1+∠PAB=90° ∵AD是⊙O的直径
∴∠1+∠D=90° ∴∠PAB=∠D 又∵∠C=∠D ∴∠PAB=∠C
又∵∠P=∠P ∴△PAB∽△PCA.
(3)1.


 学业测评一课一测系列答案
学业测评一课一测系列答案科目:初中数学 来源: 题型:
【题目】如图,已知Rt△ABC≌Rt△ADE,∠ABC=∠ADE=90°,BC与DE相交于点F,连结 CD,EB. 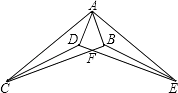
(1)不添加辅助线,找出图中其它的全等三角形;
(2)求证:CF=EF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AC⊥BC,DE⊥AB,AD平分∠BAC,下面结论错误的是( ) 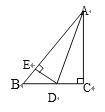
A.BD+ED=BC
B.DE平分∠ADB
C.AD平分∠EDC
D.ED+AC>AD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一只甲虫在![]() 的方格(每小格边长为
的方格(每小格边长为![]() )上沿着网格线运动,网格线与网格线的交点为格点,甲虫从
)上沿着网格线运动,网格线与网格线的交点为格点,甲虫从![]() 处出发去看望格点
处出发去看望格点![]() 、
、![]() 、
、![]() 处的其它甲虫,若规定:向上向右走均为正,向下向左走均为负,如果从
处的其它甲虫,若规定:向上向右走均为正,向下向左走均为负,如果从![]() 到
到![]() 记为:
记为:![]() ,从
,从![]() 到
到![]() 记为:
记为:![]() ,其中第一个数表示左右方向,第二个数表示上下方向.
,其中第一个数表示左右方向,第二个数表示上下方向.
(![]() )图中
)图中![]() __________.
__________.
(![]() )若这只甲虫从
)若这只甲虫从![]() 处出发,行走路线依次为
处出发,行走路线依次为![]() ,
,![]() ,
,![]() ,
,![]() ,最后在
,最后在![]() 点停止运动,请在图中标出点
点停止运动,请在图中标出点![]() 的位置.
的位置.
(![]() )若这只甲虫的行走路线为
)若这只甲虫的行走路线为![]() ,则该甲虫走过的路程长度为__________.
,则该甲虫走过的路程长度为__________.
(![]() )若图中另有两个格点
)若图中另有两个格点![]() 、
、![]() ,且
,且![]() ,
,![]() ,则
,则![]() 应记为__________.
应记为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把小圆形场地的半径增加5米得到大圆形场地,此时大圆形场地的面积是小圆形场地的4倍,设小圆形场地的半径为x米,若要求出未知数x,则应列出方程 (列出方程,不要求解方程).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com