练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
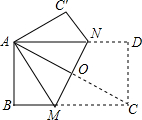
    11．如图，在矩形ABCD中，AD＞AB，点M，N分别在BC，AD边上，将矩形ABCD以直线MN为折痕进行折叠，翻折后能使点C恰好与A点重合，△AMN是一个怎样的三角形？请说明理由．

    分析 由翻折的性质可知：AO=OC，AM=MC．然后证明依据AAS证明△ANO≌△CMO，故此AN=MC，于是得到AM=AN．

    解答 解：△AMN是等腰三角形．
    理由：由翻折的性质可知：AO=OC，AM=MC．
    ∵AD∥BC，
    ∴∠ANO=∠CMO．
    在△ANO和△CMO中，
    $\left\{\begin{array}{l}{∠ANO=∠CMO}\\{∠AON=∠COM}\\{AO=OC}\end{array}\right.$，
    ∴△ANO≌△CMO．
    ∴AN=MC．
    ∴AM=AN．
    ∴△AMN是等腰三角形．

    点评 本题主要考查的是翻折的性质、全等三角形的性质和判定，证得△ANO≌△CMO是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    5．化简：（-$\frac{3{m}^{2}n}{m+n}$）3=-$\frac{27{m}^{6}{n}^{3}}{（m+n）^{3}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．已知|2x-4|+（y+3）2=0．则x+y的值是-1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．已知a=$\frac{\sqrt{2}-1}{\sqrt{2}+1}$，b=$\frac{\sqrt{2}+1}{\sqrt{2}-1}$，求$\frac{b}{a}$+$\frac{a}{b}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

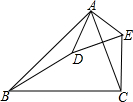    6．如图所示，△ABC∽△ADE．求证：
    （1）∠BAD=∠CAE，$\frac{AB}{AC}$=$\frac{AD}{AE}$；
    （2）∠ABD=∠ACE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．在Rt△ABC中，已知∠B=90°，AC=10，AB=5$\sqrt{2}$，则∠A等于（　　）
    A．45°B．30°C．60°D．50°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．如图，△ABE和△ACD是△ABC分别沿着AB、AC边翻折180°形成的，若∠BAC=150°，求∠θ的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    20．下列不等式中，是一元一次不等式的是（　　）
    A．2（1-y）+y＞4y+2B．x（x-5）≥4C．$\frac{1}{2}-\frac{1}{4}＞\frac{1}{5}$D．y+1＜y+2

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．在10张奖券中，有4张有奖，从中任抽一张，能中奖的概率为（　　）
    A．$\frac{4}{10}$B．$\frac{4}{5}$C．$\frac{3}{5}$D．$\frac{2}{5}$

    查看答案和解析>>

    同步练习册答案