
科目:初中数学 来源: 题型:选择题
| A. | 1.94×109 | B. | 0.194×1010 | C. | 19.4×109 | D. | 1.94×1010 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 2014年,山西省某地实施了“免费校车工程”.小明原来骑自行车上学,现在乘校车上学可以从家晚10分钟出发,结果与原来到校时间相同.已知小明家距学校5千米,若校车速度是他骑车速度的2倍,设小明骑车的速度为x千米/小时,则所列方程正确的为( )
2014年,山西省某地实施了“免费校车工程”.小明原来骑自行车上学,现在乘校车上学可以从家晚10分钟出发,结果与原来到校时间相同.已知小明家距学校5千米,若校车速度是他骑车速度的2倍,设小明骑车的速度为x千米/小时,则所列方程正确的为( )| A. | $\frac{5}{x}$+$\frac{1}{6}$=$\frac{5}{2x}$ | B. | $\frac{5}{x}$=$\frac{5}{2x}$+$\frac{1}{6}$ | C. | $\frac{5}{x}$+10=$\frac{5}{2x}$ | D. | $\frac{5}{x}$-10=$\frac{5}{2x}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
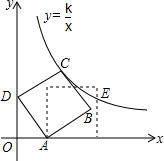 如图,在平面直角坐标系中,边长为2的正方形ABCD斜靠在y轴上,顶点A(1,0),反比例函数y=$\frac{k}{x}$图象经过点C,将正方形ABCD绕点A顺时针旋转一定角度后,使得点B恰好落在x轴的正半轴上,此时边BC交反比例图象于点E,则点E的纵坐标是( )
如图,在平面直角坐标系中,边长为2的正方形ABCD斜靠在y轴上,顶点A(1,0),反比例函数y=$\frac{k}{x}$图象经过点C,将正方形ABCD绕点A顺时针旋转一定角度后,使得点B恰好落在x轴的正半轴上,此时边BC交反比例图象于点E,则点E的纵坐标是( )| A. | $\sqrt{3}$ | B. | $\frac{1}{3}\sqrt{3}+1$ | C. | $\frac{1}{2}\sqrt{3}+1$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
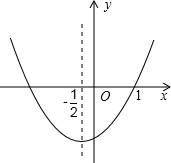 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为直线x=-$\frac{1}{2}$,有下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为直线x=-$\frac{1}{2}$,有下列结论:| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com