
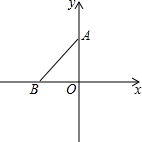
 如图,在直角坐标平面内有两点A(0,2)、B(-2,0),且A、B两点之间的距离等于a(a为大于0的已知数),在不计算a的数值的条件下,完成下列问题:
如图,在直角坐标平面内有两点A(0,2)、B(-2,0),且A、B两点之间的距离等于a(a为大于0的已知数),在不计算a的数值的条件下,完成下列问题:科目:初中数学 来源: 题型:选择题
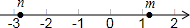 如图,点M、N在数轴上表示的数分别是m,n,则下列式子中成立的是( )
如图,点M、N在数轴上表示的数分别是m,n,则下列式子中成立的是( )| A. | m-n>0 | B. | |n|-|m|<0 | C. | m+3<n+3 | D. | -m>-n |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为了探究代数式$\sqrt{{x^2}+4}+\sqrt{{{({9-x})}^2}+1}$的最小值,小明巧妙的运用了“数形结合”思想.具体方法是这样的:如图,C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC.已知AB=2,DE=1,BD=9,设BC=x.则$AC=\sqrt{{x^2}+4}$,$CE=\sqrt{{{({9-x})}^2}+1}$,则问题即转化成求AC+CE的最小值.
为了探究代数式$\sqrt{{x^2}+4}+\sqrt{{{({9-x})}^2}+1}$的最小值,小明巧妙的运用了“数形结合”思想.具体方法是这样的:如图,C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC.已知AB=2,DE=1,BD=9,设BC=x.则$AC=\sqrt{{x^2}+4}$,$CE=\sqrt{{{({9-x})}^2}+1}$,则问题即转化成求AC+CE的最小值.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
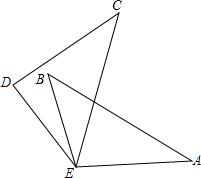 如图,已知△EAB≌△DCE,AB、EC分别是两个三角形的最长边,∠A=∠C=35°,∠CDE=100°,∠DEB=10°,求∠AEC的度数.
如图,已知△EAB≌△DCE,AB、EC分别是两个三角形的最长边,∠A=∠C=35°,∠CDE=100°,∠DEB=10°,求∠AEC的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 运往甲地 | 运往乙地 | |
| A | ||
| B |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com