
分析 (1)首先用未知数表示出包装为2吨的件数,然后根据两种包装的总重量为60吨,来表示出包装为3吨的件数;然后根据“包装成本不少于1700元,但又不多于1800元”以及“2吨包装的货物总量不少于40吨”,列出不等式组,求出未知数的取值范围,由于件数必须使正整数,可据此求出x的整数值,从而确定出有几种包装方案.
(2)根据(1)得到的包装方案以及题目给出的各种包装的单件成本,列式求出各种方案所需成本,即可得到包装成本最低的方案以及成本的最低值.
(3)根据(1)得到的包装为2吨、3吨的件数表达式,结合各种包装的单件获利额,即可表示出两种包装总的获利额,由此得关于总的获利额和(1)所设未知数的函数关系式,根据函数的性质即可确定出获利最多的包装方案.
解答 解:(1)设2吨装x件,3吨装的$\frac{60-2x}{3}$件
由题意,得$\left\{\begin{array}{l}{1700≤60x+\frac{60-2x}{3}×80≤1800}\\{2x≥40}\end{array}\right.$,
解得,20≤x≤30,∵$\frac{60-2x}{3}$是正整数,
∴有三种包装方案:
①x=21,y=6,②x=24,y=4,③x=27,y=2.
(2)∵21×60+6×80=1740,
24×60+4×80=1760,
27×60+2×80=1780,
∴2吨装21件,3吨装6件成本最低,最低成本1740元.
(3)设利润为W元,$W=200a+270×\frac{60-2a}{3}$=20a+5400;
∴当a=27时,W最大=20×27+5400=5940;
答:应用方案③:2吨装27件,3吨装2件获利最大,此时a的值是27.
点评 此题主要考查了一次函数的应用,关键是根据一元一次不等式组的实际应用以及一次函数最值的应用分析.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
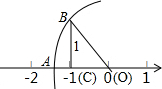 如图,直角三角形OBC中,BC=1,OC在数轴上,且点O、C对应的实数分别是0,-1,以点O为圆心,OB的长为半径画弧,与数轴的负半轴交于点A,设点A所对应的实数为x,则x2-10的立方根为( )
如图,直角三角形OBC中,BC=1,OC在数轴上,且点O、C对应的实数分别是0,-1,以点O为圆心,OB的长为半径画弧,与数轴的负半轴交于点A,设点A所对应的实数为x,则x2-10的立方根为( )| A. | $\sqrt{2}$-10 | B. | -$\sqrt{2}$-10 | C. | 2 | D. | -2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
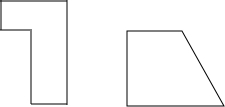 某公园准备用如图所示的材料给一块矩形的场地铺地面
某公园准备用如图所示的材料给一块矩形的场地铺地面查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4 | B. | 6 | C. | 8 | D. | 12 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com