
分析 由过△ABC的重心作DE∥BC,可得$\overrightarrow{DE}$=$\frac{2}{3}$$\overrightarrow{BC}$,再利用三角形法则求解即可求得答案.
解答 解:∵过△ABC的重心作DE∥BC,
∴$\frac{DE}{BC}$=$\frac{2}{3}$,
∴$\overrightarrow{DE}$=$\frac{2}{3}$$\overrightarrow{BC}$=$\frac{2}{3}$($\overrightarrow{AC}$-$\overrightarrow{AB}$)=$\frac{2}{3}$$\overrightarrow{b}$-$\frac{2}{3}$$\overrightarrow{a}$.
故答案为:$\frac{2}{3}$$\overrightarrow{b}$-$\frac{2}{3}$$\overrightarrow{a}$.
点评 此题考查了平面向量的知识以及三角形重心的性质.注意掌握三角形法则的应用.


科目:初中数学 来源: 题型:选择题
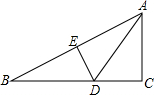 如图,△ABC中,∠ACB=90°,∠B=30°,DE垂直平分AB,若DE=1.5cm,则BC的长是( )
如图,△ABC中,∠ACB=90°,∠B=30°,DE垂直平分AB,若DE=1.5cm,则BC的长是( )| A. | 3cm | B. | 4.5cm | C. | 6cm | D. | 7.5cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
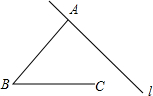 如图所示的平面图形中,下列说法错误的是( )
如图所示的平面图形中,下列说法错误的是( )| A. | 直线l经过点A | B. | 射线BC不与直线l相交 | ||
| C. | 点B在直线l外 | D. | 点A到点B的距离是线段AB的长度 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
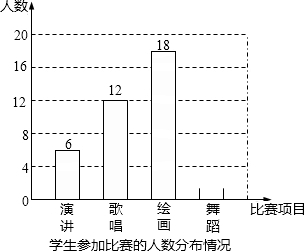 双城区某中学为了丰富校园文化生活,校学生会决定举办演讲、歌唱、绘画、舞蹈四项比赛,要求每位学生都参加.且只能参加一项比赛.围绕“你参赛的项目是什么?(只写一项)”的问题,校学生会在全校范围内随机抽取部分学生进行问卷调查.将调查问卷适当整理后绘制成如图所示的不完整的条形统计图.其中参加舞蹈比赛的人数与参加歌唱比赛的人数之比为1:3.请你根据以上信息回答下列问题:
双城区某中学为了丰富校园文化生活,校学生会决定举办演讲、歌唱、绘画、舞蹈四项比赛,要求每位学生都参加.且只能参加一项比赛.围绕“你参赛的项目是什么?(只写一项)”的问题,校学生会在全校范围内随机抽取部分学生进行问卷调查.将调查问卷适当整理后绘制成如图所示的不完整的条形统计图.其中参加舞蹈比赛的人数与参加歌唱比赛的人数之比为1:3.请你根据以上信息回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 15 | B. | 115 | C. | 225 | D. | 625 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com