
 如图,在△ABC中,GD⊥AC于点D,∠AFE=∠ABC,∠1+∠2=180°,∠AEF=65°.求:∠1的度数.
如图,在△ABC中,GD⊥AC于点D,∠AFE=∠ABC,∠1+∠2=180°,∠AEF=65°.求:∠1的度数. 科目:初中数学 来源: 题型:填空题
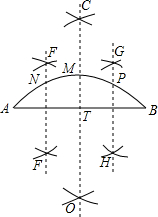 小明四等分弧AB,他的作法如下:
小明四等分弧AB,他的作法如下:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
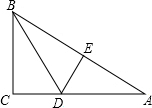 如图,在Rt△ABC中,∠C=90°,把AB对折后,点A与点B重合,折痕为DE.
如图,在Rt△ABC中,∠C=90°,把AB对折后,点A与点B重合,折痕为DE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某公司欲招聘职员一名,对甲乙丙三名候选人进行了笔试和面试两项测试,其成绩如表所示:根据录用程序,该单位又组织了100名评议人员对三人进行投票测评,其得票率如扇形图所示,每票得2分(没有弃权票,每人只能1投票)
某公司欲招聘职员一名,对甲乙丙三名候选人进行了笔试和面试两项测试,其成绩如表所示:根据录用程序,该单位又组织了100名评议人员对三人进行投票测评,其得票率如扇形图所示,每票得2分(没有弃权票,每人只能1投票)| 测试项目 | 测试成绩分 | ||
| 甲 | 乙 | 丙 | |
| 笔试 | 80 | 85 | 95 |
| 面试 | 98 | 75 | 73 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -1 | B. | $\frac{1}{2}$ | C. | 3.$\stackrel{•}{1}$$\stackrel{•}{4}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,抛物线y=-$\frac{1}{2}$x2+$\frac{7}{2}$x与矩形OABC的边AB交于点D、B,A(0,3),C(6,0),则图中抛物线与矩形OABC形成的阴影部分的面积的和为( )
如图,抛物线y=-$\frac{1}{2}$x2+$\frac{7}{2}$x与矩形OABC的边AB交于点D、B,A(0,3),C(6,0),则图中抛物线与矩形OABC形成的阴影部分的面积的和为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com