
 某公司欲招聘职员一名,对甲乙丙三名候选人进行了笔试和面试两项测试,其成绩如表所示:根据录用程序,该单位又组织了100名评议人员对三人进行投票测评,其得票率如扇形图所示,每票得2分(没有弃权票,每人只能1投票)
某公司欲招聘职员一名,对甲乙丙三名候选人进行了笔试和面试两项测试,其成绩如表所示:根据录用程序,该单位又组织了100名评议人员对三人进行投票测评,其得票率如扇形图所示,每票得2分(没有弃权票,每人只能1投票)| 测试项目 | 测试成绩分 | ||
| 甲 | 乙 | 丙 | |
| 笔试 | 80 | 85 | 95 |
| 面试 | 98 | 75 | 73 |
分析 (1)根据民主评议人员和所占的比直接求解;
(2)将笔试、面试、民主评议三项测试得分按2:1:2算出成绩,分最高的将被录取.
解答 解:(1)甲民主评议得分:100×25%=25分;
乙民主评议得分:100×40%=40分;
丙民主评议得分:100×35%=35分;
(2)甲的成绩:80×$\frac{2}{5}$+98×$\frac{1}{5}$+25×$\frac{2}{5}$=61.6分;
乙的成绩:85×$\frac{2}{5}$+75×$\frac{1}{5}$+40×$\frac{2}{5}$=65分;
丙的成绩:95×$\frac{2}{5}$+73×$\frac{1}{5}$+35×$\frac{2}{5}$=66.6分.
所以丙将被录用,因为丙的成绩最好.
点评 本题考查了加权平均数的概念及求法,属于基础题,牢记加权平均数的计算公式是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
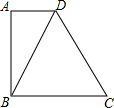 如图所示,在四边形ABCD中,AB⊥BC,AB⊥AD,BD=BC,∠C=60°,如果△DBC的周长为m,则AD的长为( )
如图所示,在四边形ABCD中,AB⊥BC,AB⊥AD,BD=BC,∠C=60°,如果△DBC的周长为m,则AD的长为( )| A. | $\frac{m}{3}$ | B. | $\frac{m}{6}$ | C. | $\frac{m}{8}$ | D. | $\frac{m}{12}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,有三个村庄分别是A、B、C,现计划修建一个居民活动中心P,要求到三个村庄的距离相等,请在图中确定活动中心P的位置.
如图,有三个村庄分别是A、B、C,现计划修建一个居民活动中心P,要求到三个村庄的距离相等,请在图中确定活动中心P的位置.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com