
分析 (1)、(2)、(3)直接把各特殊角的三角函数值代入进行计算即可;
(4)先根据特殊角的三角函数值求出α的值,再根据0指数幂及负整数指数幂的计算法则、特殊角的三角函数值分别计算出各数,由实数混合运算的法则进行计算即可.
解答 解:(1)原式=$\sqrt{3}$×$\frac{\sqrt{3}}{2}$-2×$\frac{\sqrt{3}}{2}$
=$\frac{3}{2}$-$\sqrt{3}$;
(2)原式=$\frac{1}{4}$+$\frac{1}{2}$+$\sqrt{2}$×$\frac{\sqrt{3}}{2}$×1
=$\frac{3}{4}$+$\frac{\sqrt{6}}{2}$;
(3)原式=$\sqrt{1-2×\sqrt{3}+(\sqrt{3})^{2}}$-$\sqrt{3}$
=$\sqrt{3}$-1-$\sqrt{3}$
=-1;
(4)∵α是锐角,且sin(α+15°)=$\frac{{\sqrt{3}}}{2}$,
∴α+15°=60°,
∴α=45°,
∴原式=2$\sqrt{2}$-4×$\frac{\sqrt{2}}{2}$-1+1+3
=2$\sqrt{2}$-2$\sqrt{2}$-1+1+3
=3.
点评 本题考查的是实数的运算,熟知0指数幂及负整数指数幂的计算法则、特殊角的三角函数值是解答此题的关键.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:解答题
 某公司欲招聘职员一名,对甲乙丙三名候选人进行了笔试和面试两项测试,其成绩如表所示:根据录用程序,该单位又组织了100名评议人员对三人进行投票测评,其得票率如扇形图所示,每票得2分(没有弃权票,每人只能1投票)
某公司欲招聘职员一名,对甲乙丙三名候选人进行了笔试和面试两项测试,其成绩如表所示:根据录用程序,该单位又组织了100名评议人员对三人进行投票测评,其得票率如扇形图所示,每票得2分(没有弃权票,每人只能1投票)| 测试项目 | 测试成绩分 | ||
| 甲 | 乙 | 丙 | |
| 笔试 | 80 | 85 | 95 |
| 面试 | 98 | 75 | 73 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 德强六年级有850名同学参加课外兴趣小组,分布情况如图:
德强六年级有850名同学参加课外兴趣小组,分布情况如图:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
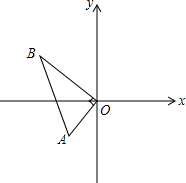 如图,在Rt△AOB中,∠AOB=90°,已知点A(-1,-1),点B在第二象限,OB=2$\sqrt{2}$,抛物线y=$\frac{3}{5}$x2+bx+c经过点A和B.
如图,在Rt△AOB中,∠AOB=90°,已知点A(-1,-1),点B在第二象限,OB=2$\sqrt{2}$,抛物线y=$\frac{3}{5}$x2+bx+c经过点A和B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com