
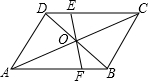
 如图,?ABCD中,EF过对角线的交点O分别与CD、AB交于点E、F,AB=4,AD=3,OF=1.3,则四边形BCEF的周长为( )
如图,?ABCD中,EF过对角线的交点O分别与CD、AB交于点E、F,AB=4,AD=3,OF=1.3,则四边形BCEF的周长为( )| A. | 8.3 | B. | 9.6 | C. | 12.6 | D. | 13.6 |
分析 由四边形ABCD是平行四边形,即可得AB=CD=4,AD=BC=3,AB∥CD,OA=OC,则易证△ECO≌△FAO,根据全等三角形的对应边相等,即可得AF=CE,OE=OF=1.3,然后求得四边形BCEF的周长,得到答案.
解答 解:∵四边形ABCD是平行四边形,
∴AB=CD=4,AD=BC=3,AB∥CD,OA=OC,
∴∠CEO=∠AFO,∠ECO=∠FAO,
在△ECO与△FAO中,
$\left\{\begin{array}{l}{∠CEO=∠AFO}\\{∠ECO=∠FAO}\\{OA=OC}\end{array}\right.$,
∴△ECO≌△FAO,
∴AF=CE,OE=OF=1.3,
∴EF=2.6,
∴四边形BCEF的周长为:BC+CE+EF+BF=BC+AF+BF+EF=BC+AB+EF=4+3+2.6=9.6.
故选B.
点评 此题考查了平行四边形的性质与全等三角形的判定与性质.此题比较简单,解题的关键是注意数形结合思想的应用.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
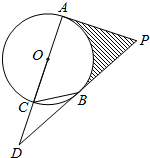 如图,已知PA、PB是⊙O的切线,A、B为切点.直径AC的延长线与PB的延长线交于点D.
如图,已知PA、PB是⊙O的切线,A、B为切点.直径AC的延长线与PB的延长线交于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为解决停车难的问题,在如图一段长56米的路段开辟停车位,每个车位是长5米、宽2.2米的矩形,矩形的边与路的边缘成45°角,那么这个路段最多可以划出17个这样的停车位($\sqrt{2}$≈1.4)
为解决停车难的问题,在如图一段长56米的路段开辟停车位,每个车位是长5米、宽2.2米的矩形,矩形的边与路的边缘成45°角,那么这个路段最多可以划出17个这样的停车位($\sqrt{2}$≈1.4)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 下面的图象反映的是小明从家跑步去图书馆,在那里锻炼了一阵后又走到文具店去买本,然后散步回家.图中x表示时间,y表示小明离家的距离.
下面的图象反映的是小明从家跑步去图书馆,在那里锻炼了一阵后又走到文具店去买本,然后散步回家.图中x表示时间,y表示小明离家的距离.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com