
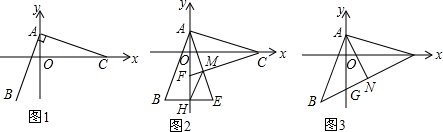
分析 (1)根据题意求得a=2,c=6,从而求得A、C的坐标,然后证得△AOC≌△BDA,求得BD=OA=2,AD=OC=6,从而求得B的坐标;
(2)分三种情况分别讨论即可求得;
(3)根据题意得出△AOC≌△FOC≌△BHA≌△EHA,得出AF=BE=4,从而得出FH=EH=2,连接EF,则∠HEF=45°,根据∠OCF+∠AFC=90°,∠HAE=∠OCF,得出∠AMF=90°,进而证得E、M、F、H四点在以EF为直径的圆上,根据圆周角定理即可证得∠HMF=∠FEH=45°;
(4)根据已知易证△ABC是等腰直角三角形,进而就可求得AB=AC=2$\sqrt{10}$,得出BC=4$\sqrt{5}$,根据等腰直角三角形的性质求得AN=BN=CN=2$\sqrt{5}$,作BD⊥y轴于D,则BD∥OC,得出$\frac{BD}{OC}$=$\frac{BG}{CG}$,求得$\frac{BG}{CG}$=$\frac{1}{3}$,即可求得NG=$\sqrt{5}$,继而求得$\frac{NC}{NG}$的值.
解答 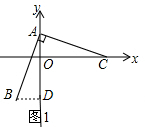 解:(1)根据题意,a2-4≥0且4-a2≥0,
解:(1)根据题意,a2-4≥0且4-a2≥0,
解得a≥2且a≤2,
所以,a=2,
c=$\frac{\sqrt{{a}^{2}-4}+\sqrt{4-{a}^{2}}+24}{a+2}$=6,
∴点A(0,2),C(6,0),
∴OA=2,OC=6,
如图1,过点B作BD⊥y轴于点D,
∵∠BAD+∠CAO=90°,∠ACO+∠CAO=90°,
∴∠ACO=∠BAD,
在△AOC和△BDA中,
$\left\{\begin{array}{l}{∠ACO=∠BAD}\\{∠AOC=∠ADB=90°}\\{AB=AC}\end{array}\right.$,
∴△AOC≌△BDA(AAS),
∴BD=OA=2,AD=OC=6,
∴OD=AD-OA=6-2=4,
∴点B的坐标为(-2,-4);
(2)第一种情况如图2,当AE=AD时,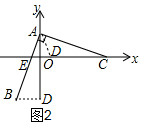
∵AO=2,AD=6,BD=2,
∴$\frac{OE}{BD}$=$\frac{AO}{AD}$,解得OE=$\frac{2}{3}$,
∴OD=$\frac{2}{3}$,
∴D($\frac{2}{3}$,0)
第二种情况,如图3,当AD=ED时,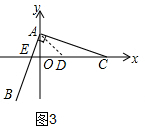
设OD=x,可得$\sqrt{{x}^{2}+{2}^{2}}$=$\frac{2}{3}$+x,解得x=$\frac{8}{3}$,
∴D($\frac{8}{3}$,0)
第三种情况,如图4,当AE=DE时,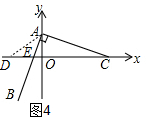
∵AE=$\sqrt{A{O}^{2}+O{E}^{2}}$=$\sqrt{{2}^{2}+(\frac{2}{3})^{2}}$=$\frac{2\sqrt{10}}{3}$,
∴OD=$\frac{2}{3}$+$\frac{2\sqrt{10}}{3}$,
∴D($\frac{2}{3}$+$\frac{2\sqrt{10}}{3}$,0);
(3)如图5,∵B,E关于y轴对称,A,F关于x轴对称,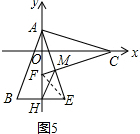
∴△AOC≌△FOC,△BHA≌△EHA,
∵△AOC≌△BHA,
∴△EHA≌△FOC,
∴EH=OF=OA=BH=2,∠HAE=∠OCF,
∵OH=4,
∴FH=2,
∴FH=EH=2,
∴∠FEH=45°,
∵∠OCF+∠AFC=90°,∠HAE=∠OCF,
∴∠HAE+∠AFC=90°,
∴∠AMF=90°,
∵∠AHE=90°,
∴E、M、F、H四点在以EF为直径的圆上,
∴∠HMF=∠FEH=45°;
(4)如图6,∵AB⊥AC,且AB=AC.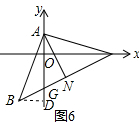
∴△ABC是等腰直角三角形,AB=AC=$\sqrt{{2}^{2}+{6}^{2}}$=2$\sqrt{10}$
∴BC=$\sqrt{2}$AC=4$\sqrt{5}$,
∵N为BC中点,
∴AN⊥BC,AN=BN=NC=$\frac{1}{2}$BC=2$\sqrt{5}$,
作BD⊥y轴于D,则BD∥OC,
∴$\frac{BD}{OC}$=$\frac{BG}{CG}$,
∵BD=2,OC=6,
∴$\frac{BG}{CG}$=$\frac{1}{3}$,
∴BG=$\frac{1}{4}$BC=$\sqrt{5}$,
∴NG=2$\sqrt{5}$-$\sqrt{5}$=$\sqrt{5}$,
∴$\frac{NC}{NG}$=$\frac{2\sqrt{5}}{\sqrt{5}}$=2.
点评 本题是一次函数的综合题,考查了三角形全等的判定和性质,等腰三角形的判定和性质,三角形相似的判定和性质勾股定理的应用等,分类讨论思想的运用是解题的关键.


科目:初中数学 来源: 题型:解答题
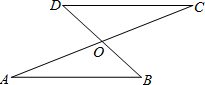 已知,如图,AC和BD相交于点O,OA=OC,OB=OD,求证:AB∥CD.
已知,如图,AC和BD相交于点O,OA=OC,OB=OD,求证:AB∥CD.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 在小明住的小区有一条笔直的路,路中间有一盏路灯,一天晚上,他行走在这条路上,如图,当他从A点走到B点的过程,他在灯光照射下的影长l与所走路程s的变化关系图象大致是( )
在小明住的小区有一条笔直的路,路中间有一盏路灯,一天晚上,他行走在这条路上,如图,当他从A点走到B点的过程,他在灯光照射下的影长l与所走路程s的变化关系图象大致是( )| A. |  | B. |  | C. | 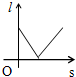 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
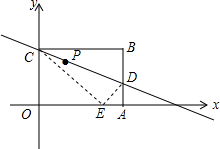 如图,在平面直角坐标系中,矩形OABC的顶点A(10,0),C(0,8),现将矩形OABC沿直线CD折叠,使点B落在x轴上的E处.
如图,在平面直角坐标系中,矩形OABC的顶点A(10,0),C(0,8),现将矩形OABC沿直线CD折叠,使点B落在x轴上的E处.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
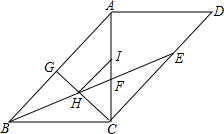 如图,平行四边形ABCD中,对角线AC⊥BC,BE平分∠ABC,交CD于点E,且与AC交于点F.过点C作CG1AB于点G,CG与BE交于点H,点I在线段AC上,且HI∥AB.求证:
如图,平行四边形ABCD中,对角线AC⊥BC,BE平分∠ABC,交CD于点E,且与AC交于点F.过点C作CG1AB于点G,CG与BE交于点H,点I在线段AC上,且HI∥AB.求证:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
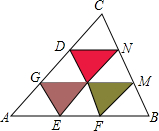 如图,在△ABC中,AB=30,BC=24,CA=27,AE=EF=FB,EG∥FD∥BC,FM∥EN∥AC,则图中阴影部分的三个三角形的周长之和为( )
如图,在△ABC中,AB=30,BC=24,CA=27,AE=EF=FB,EG∥FD∥BC,FM∥EN∥AC,则图中阴影部分的三个三角形的周长之和为( )| A. | 70 | B. | 75 | C. | 81 | D. | 80 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com