
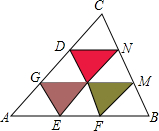
 如图,在△ABC中,AB=30,BC=24,CA=27,AE=EF=FB,EG∥FD∥BC,FM∥EN∥AC,则图中阴影部分的三个三角形的周长之和为( )
如图,在△ABC中,AB=30,BC=24,CA=27,AE=EF=FB,EG∥FD∥BC,FM∥EN∥AC,则图中阴影部分的三个三角形的周长之和为( )| A. | 70 | B. | 75 | C. | 81 | D. | 80 |
分析 设阴影部分的三个三角形的边的交点为O,由DN∥GM∥AB,EG∥DF∥BC,FM∥EN∥AC,可得四边形CDON,DFBN,OFMN,AFMG,DGEO,OGEF,GEBM是平行四边形,继而可得图中阴影部分的三个三角形周长之和为:AB+BC+AC,则可求得答案.
解答 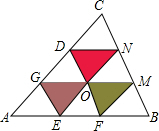 解:设阴影部分的三个三角形的边的交点为O,
解:设阴影部分的三个三角形的边的交点为O,
∵EG∥DF∥BC,FM∥EN∥AC,
∴四边形CDON,DFBN,OFMN,AFMG,DGEO,OGEF,GEBM是平行四边形,
∴ON=CD,OD=CN,DN=BF,OF=MN,OM=BF,FM=AG,OE=DG,OG=EF,GE=BM,
∴图中阴影部分的三个三角形周长之和为:AB+BC+AC=30+24+27=81.
故选C.
点评 此题考查了平行四边形的判定与性质.此题难度适中,熟练掌握平行四边形的性质定理是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
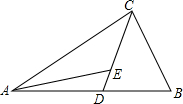 如图,△ABC中,点D在AB边上,AD=CD,点E在CD上,∠ABC+∠AEC=180°,图中是否存在与BC相等的线段?若存在,请找出,并加以证明,若不存在,请说明理由.
如图,△ABC中,点D在AB边上,AD=CD,点E在CD上,∠ABC+∠AEC=180°,图中是否存在与BC相等的线段?若存在,请找出,并加以证明,若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
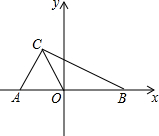 如图,在平面直角坐标系中,A(a,0),B(b,0),C(-1,2),且|a+2|+$\sqrt{b-3}$=0.
如图,在平面直角坐标系中,A(a,0),B(b,0),C(-1,2),且|a+2|+$\sqrt{b-3}$=0.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com