
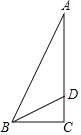
【题目】如图,△ABC中,∠C=90°,点D为AC上一点,∠ABD=2∠BAC=45°,若AD=12,则△ABD的面积为____.
【答案】36.
【解析】
作DE⊥DB交AB于E,EF垂直AC于F,则∠DEB=90°-∠ABD=45°,证出AE=DE=DB,通过证明△AEF≌△BCD,得出BC==AF=![]() AD=6,由三角形面积公式即可得出答案.
AD=6,由三角形面积公式即可得出答案.
作DE⊥DB交AB于E,EF垂直AC于F,如图所示:
则∠DEB=90°-∠ABD=45°,
∴△BDE是等腰直角三角形,
∴DB=DE,
∵∠ABD=2∠BAC=45°,
∴∠BAC=22.5°,
∴∠ADE=∠DEB-∠BAC=22.5°=∠BAC,
∴AE=DE=DB,
∵∠AFE=90°,
∴F是AD中点,AF=FD,
又∵∠C=90°,
∴∠CBD=90°-45°-22.5°=22.5°,
在Rt△AEF和Rt△BCD中

∴Rt△AEF≌Rt△BCD(AAS),
∴AF=BC=![]() AD=6,
AD=6,
∴△ABD的面积S=![]() AD×BC=
AD×BC=![]() ×12×6=36;
×12×6=36;
故答案为:36.



 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】某工厂计划生产甲、乙两种产品共2500吨,每生产1吨甲产品可获得利润0.3万元,每生产1吨乙产品可获得利润0.4万元.设该工厂生产了甲产品x(吨),生产甲、乙两种产品获得的总利润为y(万元).
(1)求y与x之间的函数表达式;
(2)若每生产1吨甲产品需要A原料0.25吨,每生产1吨乙产品需要A原料0.5吨.受市场影响,该厂能获得的A原料至多为1000吨,其它原料充足.求出该工厂生产甲、乙两种产品各为多少吨时,能获得最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,DE∥BC,点F在边AC上,DF与BE相交于点G,且∠EDF=∠ABE.

求证:(1)△DEF∽△BDE;(2)DGDF=DBEF.
查看答案和解析>>
科目:初中数学 来源: 题型:
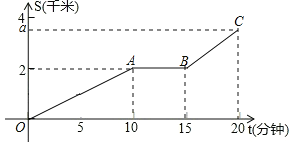
【题目】小明放学骑车回家过程中,离校的路程s与时间t的关系如图,其中小明先以平时回家的速度骑车,中间因事停留片刻,因此加快速度,请根据图象回答下列问题:
![]() 开始10分钟内的速度是多少?
开始10分钟内的速度是多少?
![]() 若小明在停留后速度每分钟加快100米,求a的值和小明平时回家所需的时间.
若小明在停留后速度每分钟加快100米,求a的值和小明平时回家所需的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电脑经销商计划购进一批电脑机箱和液晶显示器,若购电脑机箱10台和液液晶显示器8台,共需要资金7000元;若购进电脑机箱2台和液示器5台,共需要资金4120元.
(1)每台电脑机箱、液晶显示器的进价各是多少元?
(2)该经销商购进这两种商品共50台,而可用于购买这两种商品的资金不超过22240元.根据市场行情,销售电脑机箱、液晶显示器一台分别可获利10元和160元.该经销商希望销售完这两种商品,所获利润不少于4100元.试问:该经销商有哪几种进货方案?哪种方案获利最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,BC的垂直平分线DE交BC于D,交AB于E,F在DE上,且AF=CE=AE.
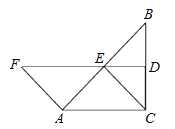
(1)说明四边形ACEF是平行四边形;
(2)当∠B满足什么条件时,四边形ACEF是菱形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:关于x的一元二次方程mx2﹣(2m﹣2)x+m=0有实根.
(1)求m的取值范围;
(2)若原方程两个实数根为x1,x2,是否存在实数m,使得![]() =1?请说明理由.
=1?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,直线y=2kx-2k (k>0)交y轴于点B,与直线y=kx交于点A.
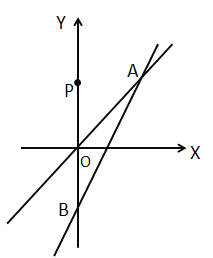
(1)求点A的横坐标;
(2)直接写出![]() 的x的取值范围;
的x的取值范围;
(3)若P(0,3)求PA+OA的最小值,并求此时k的值;
(4)若C(0,2)以A,B,C,D为顶点的四边形是以BC为一条边的菱形,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
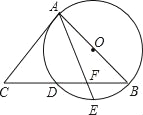
【题目】如图,AB是⊙O的直径,BC交⊙O于点D,E是![]() 的中点,AE与BC交于点F,∠C=2∠EAB.
的中点,AE与BC交于点F,∠C=2∠EAB.
(1)求证:AC是⊙O的切线;
(2)已知CD=4,CA=6,
①求CB的长;
②求DF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com