
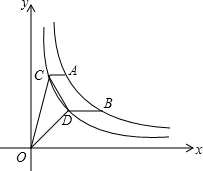
 如图,点A、B在双曲线y1=$\frac{k}{x}$(k>1,x>0)上,点C、点D在双曲线y2=$\frac{1}{x}$(x>0)上,AC∥BD∥x轴,若$\frac{AC}{BD}$=m,则△OCD的面积为$\frac{1-{m}^{2}}{2m}$.(用含m的式子表示)
如图,点A、B在双曲线y1=$\frac{k}{x}$(k>1,x>0)上,点C、点D在双曲线y2=$\frac{1}{x}$(x>0)上,AC∥BD∥x轴,若$\frac{AC}{BD}$=m,则△OCD的面积为$\frac{1-{m}^{2}}{2m}$.(用含m的式子表示) 分析 先根据反比例函数图象上点的坐标特征可设C(a,$\frac{•1}{a}$),D(b,$\frac{1}{b}$),再由A,B是函数y=$\frac{k}{x}$在第一象限图象上的两个点,AC∥BD∥x轴,得出A(ak,$\frac{1}{a}$),B(bk,$\frac{1}{b}$),那么根据$\frac{AC}{BD}$,得出a=bm.过点C作CM⊥y轴于点M,作CN⊥x轴于点N,过点D作DP⊥x轴于点P,则△COD的面积=矩形ONCM的面积+梯形PDCN的面积-△COM的面积-△DOP的面积,由反比例函数系数k的几何意义,可知矩形ONCM的面积=1,△COM的面积=△DOP的面积=$\frac{1}{2}$,所以△COD的面积=梯形PDCN的面积,根据梯形的面积公式即可求解.
解答 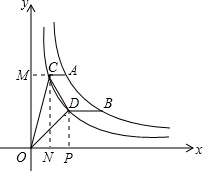 解:∵C,D是函数y=$\frac{1}{x}$上两点,
解:∵C,D是函数y=$\frac{1}{x}$上两点,
∴可设C(a,$\frac{•1}{a}$),D(b,$\frac{1}{b}$),
∵A,B是函数y=$\frac{k}{x}$在第一象限图象上的两个点,AC∥BD∥x轴,
∴A(ak,$\frac{•1}{a}$),B(bk,$\frac{1}{b}$).
∵$\frac{AC}{BD}$,
∴$\frac{ak-a}{bk-b}$=m,
由图可知k≠1,
∴a=bm.
如图,过点C作CM⊥y轴于点M,作CN⊥x轴于点N,过点D作DP⊥x轴于点P,
则S△COD=S矩形ONCM+S梯形PDCN-S△COM-S△DOP
=1+$\frac{1}{2}$($\frac{1}{b}$+$\frac{•1}{a}$)•(b-a)-$\frac{1}{2}$-$\frac{1}{2}$
=$\frac{1}{2}$($\frac{1}{b}$+$\frac{1}{bm}$)•(b-bm)
=$\frac{1-{m}^{2}}{2m}$.
故答案为$\frac{1-{m}^{2}}{2m}$.
点评 本题考查了反比例函数图象上点的坐标特征,平行于坐标轴的直线上点的坐标特征,反比例函数系数k的几何意义,三角形的面积,有一定难度.运用数形结合的思想,准确地设出点的坐标是解题的关键.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
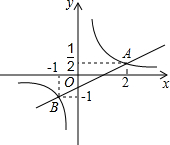 如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象相交于A(2,$\frac{1}{2}$),B(-1,1)两点.
如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象相交于A(2,$\frac{1}{2}$),B(-1,1)两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
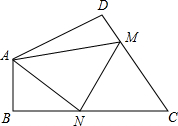 如图,在四边形ABCD中,∠DAB=130°,∠D=∠B=90°,点M,N分别是CD,BC上两个动点,当△AMN的周长最小时,∠AMN+∠ANM的度数为( )
如图,在四边形ABCD中,∠DAB=130°,∠D=∠B=90°,点M,N分别是CD,BC上两个动点,当△AMN的周长最小时,∠AMN+∠ANM的度数为( )| A. | 90° | B. | 100° | C. | 130° | D. | 140° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com