
分析 (1)用平方差和完全平方公式展开后合并同类项即可化简原式;
(2)把a=-1,b=3代入(1)中化简后的代数式即可得;
(3)将(1)中化简后的代数式除以单项式-$\frac{1}{2}$a可得结果,判断即可.
解答 解:(1)原式=a2-b2+a2-6ab+9b2-8b2
=2a2-6ab;
(2)当a=-1,b=3时,
原式=2×(-1)2-6×(-1)×3
=2+18
=20;
(3)根据题意,(2a2-6ab)÷(-$\frac{1}{2}$a)
=-4a+12b,
故这个代数式除以单项式-$\frac{1}{2}$a,所得的商是整式.
点评 本题主要考查整式的化简求值,熟练掌握整式的运算法则和平方差公式、完全平方公式是解题根本和关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
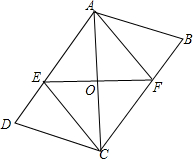 如图.四边形ABCD中,AB=CD,AD=BC,对角线AC的中点为O,过点O的直线分别交AD、BC于点E、F.
如图.四边形ABCD中,AB=CD,AD=BC,对角线AC的中点为O,过点O的直线分别交AD、BC于点E、F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图是“赵爽弦图”,△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形,如果AB=10,EF=2,求AH的长.
如图是“赵爽弦图”,△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形,如果AB=10,EF=2,求AH的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
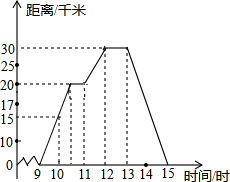 小樱某天上午9时骑自行车离开家,下午15时回到家,如图所示是小樱离家的距离与时间的变化图象.
小樱某天上午9时骑自行车离开家,下午15时回到家,如图所示是小樱离家的距离与时间的变化图象.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
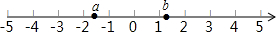 已知:实数a,b在数轴上的位置如图所示,化简:$\sqrt{(a+1)^{2}}$+2$\sqrt{(b-1)^{2}}$-|a-b|.
已知:实数a,b在数轴上的位置如图所示,化简:$\sqrt{(a+1)^{2}}$+2$\sqrt{(b-1)^{2}}$-|a-b|.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com