二次函数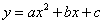
（a，b，c为常数，且a≠0）中的x与y的部分对应值如下表：
| X | ﹣1 | 0 | 1 | 3 |
| y | ﹣1 | 3 | 5 | 3 |
下列结论：
（1）ac＜0；（2）当x＞1时，y的值随x值的增大而减小．
（3）3是方程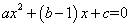
的一个根；
（4）当﹣1＜x＜3时，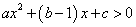
．
其中正确的个数为（ ）
A．4个 B．3个 C．2个 D．1个
科目：初中数学 来源： 题型：
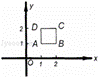
如图17，有一种动画程序，屏幕上正方形ABCD是黑色区域（含正方形边界），其中A（1，1），B（2，1），C（2，2），D（1，2），用信号枪沿直线y=﹣2x+b发射信号，当信号遇到黑色区域时，区域便由黑变白，则能够使黑色区域变白的b的取值范围为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
已知：在平面直角坐标系xoy中，抛物线y=ax2＋bx＋c与直线y=mx＋n相交于
A(0，－
),B(m－b，m2－mb＋n)两点,其中a，b，c，m，n均为实数，且a≠0，m≠0
(1) ①填空：c= ，n= ；
②求a的值。
小明思考：∵B(m－b，m2－mb＋n) 在抛物线y=ax2＋bx＋c上
∴m2－mb＋n=a(m－b)2+b(m－b)+c
……
请根据小明的解题过程直接写出a 的值：a = ___________.
(2) 若m=1，b=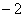
,设点P在抛物线y=ax2＋bx＋c上，且在直线AB的下方，求△ABP
面积的取值范围；
(3) 当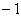
≤ x ≤1时，求抛物线y=ax2＋bx＋c上到x轴距离最大的点的坐标。（用含b的代数式表示）
 |
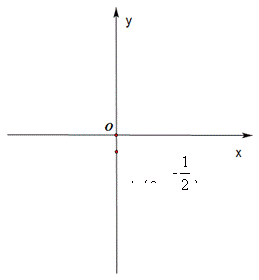查看答案和解析>>
科目：初中数学 来源： 题型：
已知：如图，一次函数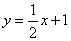
的图像与x轴交于点A，与y轴交于点B，二次函数
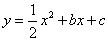的图像与一次函数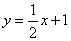的图像相交于B、C两点，与x轴
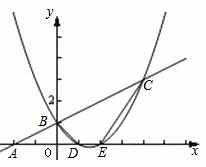
交于D、E两点且D点坐标为（1，0）.
（1）求二次函数的解析式；
（2）求四边形BDEC的面积S；
（3）在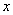
轴上是否存在点P.，使△PBC是以P为直角顶点的直角三角
形？若存在，求出所有的点P的坐标，若不存在，请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
已知直角梯形ABCO的底边AO在x轴上，BC//AO，AB⊥AO，对角线AC、BO相交于点D，双曲线y＝
经过点D，若AO＝2BC，△BCD的面积为3，则k的值为_______．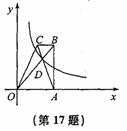
查看答案和解析>>
科目：初中数学 来源： 题型：
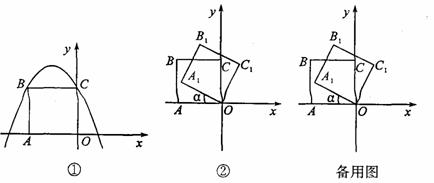
如图①，在平面直角坐标系中，二次函数y＝－x2－2x＋2的图像与y轴交于点C，以OC为一边向左侧作正方形OCBA．
(1)判断点B是否在二次函数y＝－x2－2x＋2的图像上，并说明理由；
(2)用配方法求二次函数y＝－x2－2x＋2的图像的对称轴；
(3)如图②，把正方形OCBA绕点O顺时针旋转a后得到正方形A1B1C1O(0°<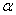
<90°)．
①当tan＝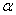
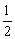时，二次函数y＝－x2－2x＋2的图像的对称轴上是否存在一点P，使△PB1C1为直角三角形？若存在，请求出所有点P的坐标；若不存在，请说明理由，
②在二次函数y＝－x2－2x＋2的图像的对称轴上是否存在一点P，使△PB1C1为等腰直角三角形？若存在，请直接写出此时tan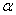的值；若不存在，请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
有解，则实数a的取值范围是（ ）
与x轴、y轴分别交于A、B两点，把△AOB绕点A顺时针旋转90°后得
，则点
的坐标是 