
分析 先解不等式组得到a≤t≤$\frac{3}{2}$,再根据不等式整数解的个数得到-2<a≤-1,然后根据一次函数图象与系数的关系求解.
解答 解:解不等式组$\left\{\begin{array}{l}{t-a≥0}\\{2t+1≤4}\end{array}\right.$得a≤t≤$\frac{3}{2}$
由于不等式组恰有三个整数,
所以-2<a≤-1,
所以一次函数y=$\frac{1}{4}$x-a的图象经过第一、二、三象限,不经过第四象限.
故答案为四.
点评 本题考查了一次函数图象与系数的关系:由于y=kx+b与y轴交于(0,b),当b>0时,(0,b)在y轴的正半轴上,直线与y轴交于正半轴;当b<0时,(0,b)在y轴的负半轴,直线与y轴交于负半轴.k>0,b>0?y=kx+b的图象在一、二、三象限;k>0,b<0?y=kx+b的图象在一、三、四象限;k<0,b>0?y=kx+b的图象在一、二、四象限;k<0,b<0?y=kx+b的图象在二、三、四象限.也考查了一元一次不等式组的整数解.


科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{8}-\sqrt{3}=\sqrt{5}$ | B. | $\sqrt{4}+\sqrt{9}=\sqrt{13}$ | C. | $3\sqrt{2}-\sqrt{2}=2\sqrt{2}$ | D. | $2+\sqrt{2}=2\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x3-x=x(x+1)(x-1) | B. | x2+2x+1=x(x+2)+1 | C. | (x+1)(x+3)=x2+4x+3 | D. | a(x-y)=ax-ay |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
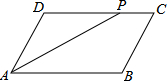 如图,平行四边形ABCD中,AB=18cm,PC=6cm,AP是∠DAB的平分线,则平行四边形ABCD的周长为( )
如图,平行四边形ABCD中,AB=18cm,PC=6cm,AP是∠DAB的平分线,则平行四边形ABCD的周长为( )| A. | 60cm | B. | 48cm | C. | 36cm | D. | 64cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
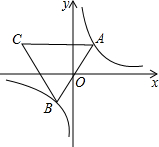 已知点A是双曲线y=$\frac{2}{x}$在第一象限上的动点,连接AO并延长交另一分支于点B,以AB为一边作等边三角形ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为( )
已知点A是双曲线y=$\frac{2}{x}$在第一象限上的动点,连接AO并延长交另一分支于点B,以AB为一边作等边三角形ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为( )| A. | y=-$\frac{2}{x}$(x<0) | B. | y=-$\frac{4}{x}$(x<0) | C. | y=-$\frac{6}{x}$(x<0) | D. | y=-$\frac{8}{x}$(x<0) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com