
分析 不等式整理后,分t+3大于等于0与小于两种情况,求出解集即可.
解答 解:不等式整理得:|t+3|≤$\frac{3}{2}$,
当t+3≥0,即t≥-3时,不等式变形得:t+3≤$\frac{3}{2}$,
解得:t≤-$\frac{3}{2}$,此时解集为-3≤t≤-$\frac{3}{2}$;
当t+3<0,即t<-3时,不等式变形得:-t-3≤$\frac{3}{2}$,
解得:t≥-$\frac{9}{2}$,此时解集为-$\frac{9}{2}$≤t<-3,
综上,不等式的解集为-$\frac{9}{2}$≤t≤-$\frac{3}{2}$.
点评 此题考查了解一元一次不等式,熟练掌握运算法则是解本题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
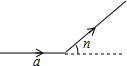 小明同学在社团活动中给发明的机器人设置程序:(a,n).机器人执行步骤是:向正前方走am后向左转n°,再依次执行相同程序,直至回到原点.现输入a=6,n=40,那么机器人回到原点共走了54m.
小明同学在社团活动中给发明的机器人设置程序:(a,n).机器人执行步骤是:向正前方走am后向左转n°,再依次执行相同程序,直至回到原点.现输入a=6,n=40,那么机器人回到原点共走了54m.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
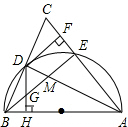 如图,在△ABC中,AB=AC,以AB为直径的半圆O交BC于点D,交AC于点E,连接AD、BE交于点M,过点D作DH⊥AB于点H,交BE于点G,有下列结论:①BD=CD;②DF是⊙O的切线;③∠DAC=∠BDH;④BM=2DG.其中,成立的个数为( )
如图,在△ABC中,AB=AC,以AB为直径的半圆O交BC于点D,交AC于点E,连接AD、BE交于点M,过点D作DH⊥AB于点H,交BE于点G,有下列结论:①BD=CD;②DF是⊙O的切线;③∠DAC=∠BDH;④BM=2DG.其中,成立的个数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
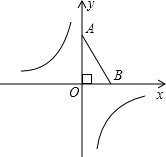 如图,平面直角坐标系中,已知点O(0,0),A(0,2),B(1,0),双曲线y=-$\frac{1}{x}$,动点P在双曲线上,PQ⊥x轴于Q,若△OPQ与△OAB相似,则满足题意的点P一共有($\sqrt{2}$,-$\frac{\sqrt{2}}{2}$)或(-$\sqrt{2}$,$\frac{\sqrt{2}}{2}$)或($\frac{\sqrt{2}}{2}$,-$\sqrt{2}$)或(-$\frac{\sqrt{2}}{2}$,$\sqrt{2}$).
如图,平面直角坐标系中,已知点O(0,0),A(0,2),B(1,0),双曲线y=-$\frac{1}{x}$,动点P在双曲线上,PQ⊥x轴于Q,若△OPQ与△OAB相似,则满足题意的点P一共有($\sqrt{2}$,-$\frac{\sqrt{2}}{2}$)或(-$\sqrt{2}$,$\frac{\sqrt{2}}{2}$)或($\frac{\sqrt{2}}{2}$,-$\sqrt{2}$)或(-$\frac{\sqrt{2}}{2}$,$\sqrt{2}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 产品 | 每件产品的产量 | 每件产品用工时数 |
| 甲 | 45万元 | 150 |
| 乙 | 75万元 | 190 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com