
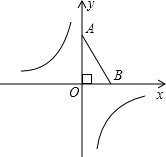
 如图,平面直角坐标系中,已知点O(0,0),A(0,2),B(1,0),双曲线y=-$\frac{1}{x}$,动点P在双曲线上,PQ⊥x轴于Q,若△OPQ与△OAB相似,则满足题意的点P一共有($\sqrt{2}$,-$\frac{\sqrt{2}}{2}$)或(-$\sqrt{2}$,$\frac{\sqrt{2}}{2}$)或($\frac{\sqrt{2}}{2}$,-$\sqrt{2}$)或(-$\frac{\sqrt{2}}{2}$,$\sqrt{2}$).
如图,平面直角坐标系中,已知点O(0,0),A(0,2),B(1,0),双曲线y=-$\frac{1}{x}$,动点P在双曲线上,PQ⊥x轴于Q,若△OPQ与△OAB相似,则满足题意的点P一共有($\sqrt{2}$,-$\frac{\sqrt{2}}{2}$)或(-$\sqrt{2}$,$\frac{\sqrt{2}}{2}$)或($\frac{\sqrt{2}}{2}$,-$\sqrt{2}$)或(-$\frac{\sqrt{2}}{2}$,$\sqrt{2}$). 分析 由A(0,2)、B(1,0),可求得OA与OB的长,然后分别从当$\frac{PQ}{BO}$=$\frac{OQ}{OA}$,即OQ=2PQ时,△OPQ∽△ABO与当 $\frac{PQ}{OA}$,即PQ=2OQ时,△OPQ∽△BAO去分析求解即可求得答案.
解答 解:∵A(0,2)、B(1,0),
∴OA=2,OB=1,
∵PQ⊥x轴,
∴∠PQO=∠AOB=90°,
当$\frac{PQ}{BO}$=$\frac{OQ}{OA}$,即OQ=2PQ时,△OPQ∽△ABO,
设点P(x,-$\frac{1}{2}$x),
∴-$\frac{1}{2}$x=-$\frac{1}{x}$,解得x=±$\sqrt{2}$,
∴点P的坐标为($\sqrt{2}$,-$\frac{\sqrt{2}}{2}$),(-$\sqrt{2}$,$\frac{\sqrt{2}}{2}$);
当$\frac{PQ}{AO}$=$\frac{OQ}{OB}$,即PQ=2OQ时,△OPQ∽△BAO,设点P(x,-2x),
∴-2x=-$\frac{1}{x}$,解得x=±$\frac{\sqrt{2}}{2}$.
∴点P的坐标是($\frac{\sqrt{2}}{2}$,-$\sqrt{2}$)或(-$\frac{\sqrt{2}}{2}$,$\sqrt{2}$).
综上可得,点P的坐标是($\sqrt{2}$,-$\frac{\sqrt{2}}{2}$)或(-$\sqrt{2}$,$\frac{\sqrt{2}}{2}$)或($\frac{\sqrt{2}}{2}$,-$\sqrt{2}$)或(-$\frac{\sqrt{2}}{2}$,$\sqrt{2}$).
故答案为:($\sqrt{2}$,-$\frac{\sqrt{2}}{2}$)或(-$\sqrt{2}$,$\frac{\sqrt{2}}{2}$)或($\frac{\sqrt{2}}{2}$,-$\sqrt{2}$)或(-$\frac{\sqrt{2}}{2}$,$\sqrt{2}$).
点评 此题考查的是反比例函数综合题,涉及到相似三角形的判定与性质以及反比例函数上点的性质.此题难度适中,注意掌握方程思想、分类讨论思想与数形结合思想的应用,


科目:初中数学 来源: 题型:选择题
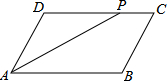 如图,平行四边形ABCD中,AB=18cm,PC=6cm,AP是∠DAB的平分线,则平行四边形ABCD的周长为( )
如图,平行四边形ABCD中,AB=18cm,PC=6cm,AP是∠DAB的平分线,则平行四边形ABCD的周长为( )| A. | 60cm | B. | 48cm | C. | 36cm | D. | 64cm |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
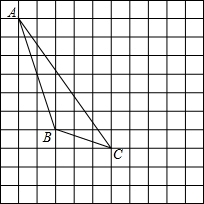 如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点.
如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
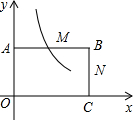 如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A、C分别在坐标轴上,顶点B的坐标为(4,2),M、N分别是AB、BC的中点.
如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A、C分别在坐标轴上,顶点B的坐标为(4,2),M、N分别是AB、BC的中点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
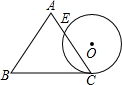 一个边长为2cm的等边三角形ABC与⊙O等高,如图放置,⊙O与BC相切于点C,⊙O与AC相交于点E,则CE的长为( )cm.
一个边长为2cm的等边三角形ABC与⊙O等高,如图放置,⊙O与BC相切于点C,⊙O与AC相交于点E,则CE的长为( )cm.| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{3}{2}$ | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com