
(本题满分12分)
如图,在平面直角坐标系中,矩形OABC的四个顶点坐标分别为O(0,0),A(4,0),B(4,3),C(0,3),G是对角线AC的中点,动直线MN平行于AC且交矩形OABC的一组邻边于E、F,交y轴、x轴于M、N.设点M的坐标为(0,t),△EFG的面积为S.

(1)求S与t的函数关系式;
(2)当△EFG为直角三角形时,求t的值;
(3)当点G关于直线EF的对称点G′ 恰好落在矩形OABC的一条边所在直线上时,直接写出t的值.
(1)S= ;(2)
;(2) 或
或 或
或 或
或 ;(3)
;(3) ,
, ,
, ,
, .
.
【解析】
试题分析:(1)分为MN在CA的左下方(0<t <3)和右上方(3<t <6)两种情况;分别把EF表示出来,并把△EFG的高表示出来即可;
(2)当0<t <3时,把△EFG三边的平方表示出来,△EFG是直角三角形有三种可能,列出三个方程,分别解出即可;同样当3<t <6时,把△EFG三边的平方表示出来,△EFG是直角三角形也有三种可能;
(3)GG’所在的直线与直线CA垂直,且过G点,故表达式为 ,分别求出直线GG’与直线CB、BA、OA、OC的交点G’,由线段GG’的中点在直线MN上即可得到四种情况的答案.
,分别求出直线GG’与直线CB、BA、OA、OC的交点G’,由线段GG’的中点在直线MN上即可得到四种情况的答案.
试题解析:
(1)①当0<t <3时,如图,过E作EH⊥CA于H,
∵A(4,0),B(4,3),C(0,3),∴OA=4,OC=3,AC=5,
∵MN∥CA,∴△OEF∽△OCA,∴OE:OC=EF:CA,即t:3=EF:5,∴EF=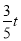 ,
,
∵EH⊥CA,∴∠ECH=∠OCA.∴sin∠ECH=sin∠OCA,∴EG:EC=OA:CA,即EH:(3-t)=4:5,∴EH= ,
,
∴S= ;
;

②当3<t <6时,如图,过C作CH⊥MN于H,

MC= ,∵CH⊥MN,∴∠CMH=∠OCA.∴sin∠CMH=sin∠OCA,
,∵CH⊥MN,∴∠CMH=∠OCA.∴sin∠CMH=sin∠OCA,
∴CH:MC=OA:CA,即CH:( )=4:5,∴EH=
)=4:5,∴EH=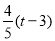 ,
,
易求直线AC的解析式为: ,∵MN∥CA,∴
,∵MN∥CA,∴ ,令y=3,∴
,令y=3,∴ ,解得:
,解得: ,∴E(
,∴E( ),在
),在 中,令
中,令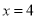 ,得:
,得: ,∴F(
,∴F( ),
),
∴EF= ,
,
∴S= ;
;
∴S= ;
;
(2)①当0<t <3时,E(0,t),F( ,0),G(2,
,0),G(2, ),
),
∴ ,
, ,
, ,
,
若 ,则:
,则: ,解得:t=0(舍去),t=
,解得:t=0(舍去),t= (舍去),
(舍去),
若 ,则:
,则: ,解得:t=0(舍去),t=
,解得:t=0(舍去),t= ,
,
若 ,则:
,则: ,解得:
,解得: ,
,
②当3<t <6时, E( ),F(
),F( ),G(2,
),G(2, ),
),
∴ ,
, ,
,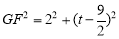 ,
,
若 ,则:
,则: ,整理得:
,整理得: ,△=441,解得:
,△=441,解得: ,t=6(舍去)
,t=6(舍去)
若 ,则:
,则: ,整理得:
,整理得: ,△=49,解得t=6(舍去),t=
,△=49,解得t=6(舍去),t= (舍去),
(舍去),
若 ,则:
,则: ,解得:
,解得: ,
,
∴ 或
或 或
或 或
或 ;
;
(3)直线MN为 ,G(2,
,G(2, ),
),
GG’所在的直线与直线CA垂直,且过G点,故表达式为 ,在
,在 中,
中,
令 ,得:
,得: ,∴G’(0,
,∴G’(0, ),GG’的中点(1,
),GG’的中点(1, ),代入直线MN为
),代入直线MN为 ,得:
,得: ,
,
令 ,得:
,得: ,∴G’(
,∴G’( ,0),GG’的中点(
,0),GG’的中点( ,
, ),代入直线MN为
),代入直线MN为 ,得:
,得: ,
,
令 ,得:
,得: ,∴G’(4,
,∴G’(4, ),GG’的中点(3,
),GG’的中点(3, ),代入直线MN为
),代入直线MN为 ,得:
,得: ,
,
令 ,得:
,得: ,∴G’(
,∴G’(  ,3),GG’的中点(
,3),GG’的中点( ,
, ),代入直线MN为
),代入直线MN为 ,得:
,得: ,
,
∴ ,
, ,
, ,
, .
.
考点:1.四边形综合题;2.直角三角形的性质.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源:2014-2015学年江苏省无锡市崇安区九年级上学期期中考试数学试卷(解析版) 题型:填空题
如图,AB、AC、BD是⊙O的切线,P、C、D为切点,如果AB=5,AC=3,则BD的长为 .

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市北塘区九年级上学期期中考试数学试卷(解析版) 题型:选择题
下面给出了一些关于相似的命题,其中真命题有( )
(1)菱形都相似;(2)等腰直角三角形都相似;(3)正方形都相似;(4)矩形都相似.
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市九年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题满分8分)电动自动车已成为市民日常出行的首选工具.据某市某品牌电动自行车经销商1至3月份统计,该品牌电动自行车1月份销售150辆,3月份销售216辆.
(1)求该品牌电动自行车销售量的月均增长率;
(2)若该品牌电动自行车的进价为2300元,售价为2800元,则该经销商1至3月共盈利多少元?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市九年级上学期期中考试数学试卷(解析版) 题型:填空题
如图,将△ABC放在每个小正方形的边长为1的网格中,点A、B、C均落在格点上,用一个圆面去覆盖△ABC,能够完全覆盖这个三角形的最小圆面的面积是 .

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市八年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题8分)如图1,四边形OABC中,OA=a,OC=5,BC=3,∠AOC=∠BCO=90°,经过点O的直线l将四边形分成两部分,直线l与OC所成的角设为θ,将四边形OABC的直角∠OCB沿直线l折叠,点C落在点D处(如图1).

(1)若折叠后点D恰为AB的中点(如图2),求θ的值;
(2)若θ=45°,四边形OABC的直角∠OCB沿直线l折叠后,点B落在点四边形OABC的边AB上,求a的值. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com