
【题目】某班数学兴趣小组经过市场调查,整理出某种商品在第![]() 天的售价与销量的相关信息如下表:
天的售价与销量的相关信息如下表:
时间 |
|
|
售价(元/件) |
| 90 |
每天销量(件) |
| |
已知该商品的进价为每件30元,设销售该商品的每天利润为![]() 元
元
(1)求出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?
【答案】(1)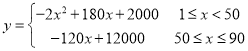 ;(2)第45天时,利润最大,为6050元;(3)41天
;(2)第45天时,利润最大,为6050元;(3)41天
【解析】
(1)根据单价乘以数量,可得利润,可得答案;
(2)根据分段函数的性质,可分别得出最大值,根据有理数的比较,可得答案;
(3)根据二次函数值大于或等于4800,一次函数值大于或等于48000,可得不等式,根据解不等式组,可得答案.
解:(1)当1≤x<50时,y=(2002x)(x+4030)=2x2+180x+2000,
当50≤x≤90时,y=(2002x)(9030)=120x+12000,
综上所述: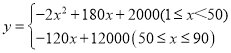 ;
;
(2)当1≤x<50时,
∴a=2<0,
∴二次函数开口下,二次函数对称轴为x=45,
当x=45时,y最大=6050,
当50≤x≤90时,y随x的增大而减小,
当x=50时,y最大=6000,
综上所述,该商品第45天时,当天销售利润最大,最大利润是6050元;
(3)①当1≤x<50时,![]() ,
,
解得:20≤x≤70,
因此利润不低于4800元的天数是20≤x<50,共30天;
②当50≤x≤90时,![]()
解得:x≤60,
因此利润不低于4800元的天数是50≤x≤60,共11天,
所以该商品在整个销售过程中,共41天每天销售利润不低于4800元.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,一段抛物线y=﹣x2+4(﹣2≤x≤2)为C1,与x轴交于A0,A1两点,顶点为D1;将C1绕点A1旋转180°得到C2,顶点为D2;C1与C2组成一个新的图象,垂直于y轴的直线l与新图象交于点P1(x1,y1),P2(x2,y2),与线段D1D2交于点P3(x3,y3),设x1,x2,x3均为正数,t=x1+x2+x3,则t的取值范围是( )

A. 6<t≤8 B. 6≤t≤8 C. 10<t≤12 D. 10≤t≤12
查看答案和解析>>
科目:初中数学 来源: 题型:
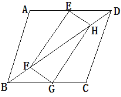
【题目】如图,矩形EFGH的顶点E,G分别在菱形ABCD的边AD,BC上,顶点F,H在菱形ABCD的对角线BD上.
(1)求证:BG=DE.
(2)若E为AD中点,FH=2,求菱形ABCD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实“精准扶贫”精神,市农科院专家指导李大爷利用坡前空地种植优质草莓.根据场调查,在草莓上市销售的30天中,其销售价格![]() (元/公斤)与第
(元/公斤)与第![]() 天之间满足
天之间满足![]() (
(![]() 为正整数),销售量
为正整数),销售量![]() (公斤)与第
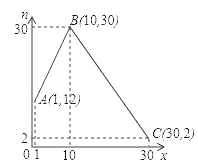
(公斤)与第![]() 天之间的函数关系如图所示:
天之间的函数关系如图所示:
如果李大爷的草莓在上市销售期间每天的维护费用为80元.
(1)求销售量![]() 与第
与第![]() 天之间的函数关系式;
天之间的函数关系式;
(2)求在草莓上市销售的30天中,每天的销售利润![]() 与第
与第![]() 天之间的函数关系式;(日销售利润=日销售额﹣日维护费)
天之间的函数关系式;(日销售利润=日销售额﹣日维护费)
(3)求日销售利润![]() 的最大值及相应的
的最大值及相应的![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在等边![]() 中,点
中,点![]() 是边
是边![]() 上一点,连接
上一点,连接![]() ,将
,将![]() 绕着点
绕着点![]() 逆时针旋转
逆时针旋转![]() ,得到
,得到![]() ,连接
,连接![]() ,则下列结论中:①
,则下列结论中:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,其中正确的结论的个数是( )
,其中正确的结论的个数是( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣(2k﹣1)x+k2+k﹣1=0有实数根.
(1)求k的取值范围;
(2)若此方程的两实数根x1,x2满足x12+x22=11,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点,连接PA,PB,AB,已知∠PBA=∠C.

(1)求证:PB是⊙O的切线;
(2)连接OP,若OP∥BC,且OP=8,⊙O的半径为![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
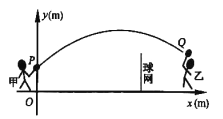
【题目】甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图,甲在![]() 点上正方
点上正方![]() 的
的![]() 处发出一球,羽毛球飞行的高度
处发出一球,羽毛球飞行的高度![]() 与水平距离
与水平距离![]() 之间满足函数表达式
之间满足函数表达式![]() .已知点
.已知点![]() 与球网的水平距离为
与球网的水平距离为![]() ,球网的高度为
,球网的高度为![]() .
.
(1)当![]() 时,①求
时,①求![]() 的值.②通过计算判断此球能否过网.
的值.②通过计算判断此球能否过网.
(2)若甲发球过网后,羽毛球飞行到点![]() 的水平距离为
的水平距离为![]() ,离地面的高度为
,离地面的高度为![]() 的
的![]() 处时,乙扣球成功,求
处时,乙扣球成功,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以△ABC的一边AB为直径作⊙O,交于BC的中点D,过点D作直线EF与⊙O相切,交AC于点E,交AB的延长线于点F.若△ABC的面积为△CDE的面积的8倍,则下列结论中,错误的是( )
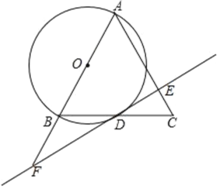
A.AC=2AOB.EF=2AEC.AB=2BFD.DF=2DE
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com