
分析 结论应用:套用上面的归纳总结代入数据,即可得出结论;
规律证明:利用上面总结的结论套入数据表示出该两个两位数的成绩,在将等式展开合并同类项得出左边=右边,从而证明结论成立.
解答 解:结论应用:352=35×35,
由3×4=12,5×5=25,得35×35=1225;
46×44,
由4×5=20,6×4=24,得46×44=2024.
故答案为:1225;2024.
规律证明:假设结论成立.
由已知得这两个两位数分别为10a+b和10a+c,
由a×(a+1)=a2+a,b×c=bc,得(10a+b)×(10a+c)=100(a2+a)+bc.
等式左边=100a2+10a(b+c)+bc,
=100a2+100a+bc,
=100(a2+a)+bc=右边.
故结论成立.
点评 本题考查了数字的变化以及新结论的应用,解题的关键:(结论应用)套入数据;(规律证明)利用分解因式法证明结论成立.本题属于基础题,难度不大,解决该题型题目时,借用给定的例题套入数据即可.


科目:初中数学 来源: 题型:解答题
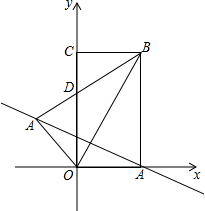 如图,矩形OABC在平面直角坐标系中,若OA,OC的长满足|OA-2|+(OC-2$\sqrt{3}$)2=0.
如图,矩形OABC在平面直角坐标系中,若OA,OC的长满足|OA-2|+(OC-2$\sqrt{3}$)2=0.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 抛物线y=-x2+x的开口向下 | |
| B. | 角平分线上的点到角两边的距离相等 | |
| C. | 一次函数y=-x+1的函数值随自变量的增大而增大 | |
| D. | 两点之间线段最短 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com