
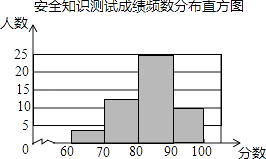
����Ŀ��ij��Ϊ���˽��������ȫ֪ʶ�����������ȡ��50�����������а�ȫ֪ʶ���ԣ��������Գɼ�����ͳ�Ʒ��������Ƴ���Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ��δ��ɣ��� ��ȫ֪ʶ���Գɼ�Ƶ���ֲ���
��� | �ɼ�x�������� | ����ֵ | Ƶ���������� |
1 | 90��x��100 | 95 | 10 |
2 | 80��x��90 | 85 | 25 |
3 | 70��x��80 | 75 | 12 |
4 | 60��x��70 | 65 | 3 |

��1�����Ƶ���ֲ�ֱ��ͼ��
��2������������ݵ���λ���ڵ��飻
��3���������������ֵ��Ϊ�����ƽ���ɼ�����˴β��Ե�ƽ���ɼ�Ϊ��
��4������90�����ϣ���90�֣���Ϊ�����㡱�ȼ��������10000���������У������㡱�ȼ���ѧ��ԼΪ�ˣ�
���𰸡�
��1���⣺���ͼ�����£�
��2��2
��3��83.4
��4��2000
���������⣺��2.���߹�50���ˣ� ����λ��Ӧ���ǵ�25�͵�26�����ݵ�ƽ������
�ߵ�25�͵�26�����ݾ����ڵ�2С�飬
����λ�����ڵ�2С�飻
��3.��ƽ����= ![]() =83.4��
=83.4��
��4.������10000���������У������㡱�ȼ���ѧ��ԼΪ10000�� ![]() =2000�ˣ�
=2000�ˣ�
���Դ��ǣ�2��83.4��2000��
�����㾫����������Ҫ������Ƶ���ֲ�ֱ��ͼ�����֪ʶ�㣬��Ҫ�����ص㣺��������ʾ�����Ƶ���ֲ��������������ʾ�����Ƶ����𣮣�ע����������ͳ��ͼ��Ƶ���ֲ�ֱ��ͼ��������ȷ�����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ��������A(a��0)��B(b��0)��C(1��3)����a��b����|3b+a��2|+![]() =0
=0
(1)��A��B�����ꣻ
(2)��x����������һ��D��ʹS��DOC=![]() S��ABC�����D���꣺
S��ABC�����D���꣺
(3)�����������Ƿ��������ĵ�D��ʹS��DOC=![]() S��ABC��Ȼ������������ֱ��д����D�����ꣻ�������ڣ�˵�����ɣ�
S��ABC��Ȼ������������ֱ��д����D�����ꣻ�������ڣ�˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧ����ϣ���ʦ�������ɸ���ͼ1������ֽƬ��A��ֽƬ�߳�Ϊa�������Σ�B��ֽƬ�DZ߳�Ϊb�������Σ�C��ֽƬ��Ϊa����Ϊb�ij����Σ�����A��ֽƬһ�ţ�B��ֽƬ�ţ�C��ֽƬ����ƴ����ͼ2�Ĵ������Σ�

��1���������ֲ�ͬ�ķ�����ͼ2�������ε������
����1���� ��������2���� ��
��2���۲�ͼ2������д��������������ʽ����a+b��2��a2+b2��ab֮��ĵ�����ϵ���� ��
��3�����ݣ�2�����еĵ�����ϵ������������⣺
����֪��a+b=5��a2+b2=11����ab��ֵ��
����֪��2018��a��2+��a��2017��2=5����2018��a����a��2017����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1������ABC�У�AB=AC����D��BC���е㣬��E��AD�ϣ�

��1����֤��BE=CE��
��2����ͼ2����BE���ӳ��߽�AC�ڵ�F����BF��AC������ΪF����BAC=45�㣬ԭ���������������䣮��֤����AEF�ա�BCF��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ж�����˵������(1)����һ�����ݣ���ô�������ݵ������п��ܲ�Ψһ________������________(2)����һ�����ݣ���ô�������ݵ�ƽ����һ�������������е�һ����________��
����________(3)n��������λ��һ������n�����е�ijһ��________������________(4)��9�����ݣ�x1��x2��������x9 �� ��ƽ����Ϊm���ı���S�� ���㹫ʽΪ��![]() ________������________
________������________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ��ֱ��������ֽƬOAB��������AOB=90�㣬OA=2��OB=4����ͼ������ֽƬ������ƽ��ֱ������ϵ�У��۵���ֽƬ���ۺ����OB���ڵ�C�����AB���ڵ�D��
��1�����۵���ʹ��B���A�غϣ����C�����꣮
��2�����۵����B���ڱ�OA�ϵĵ�ΪB�����Ƿ���ڵ�B����ʹ���ı���BCB��D�����Σ������ڣ���˵�����ɲ�������εı߳����������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���ڵ�������ABCD�У���B=60�㣬P��Qͬʱ��B��������ÿ��1����λ���ȷֱ���B��A��D��C��B��C��D�����˶�������ʱֹͣ�����˶�ʱ��Ϊt���룩����BPQ�����ΪS��ƽ����λ����S��t�ĺ���ͼ����ͼ2�������н��۴�����ǣ� ��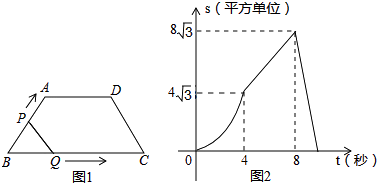
A.��t=4��ʱ��S=4 ![]()
B.AD=4
C.��4��t��8ʱ��S=2 ![]() t
t
D.��t=9��ʱ��BPƽ������ABCD�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
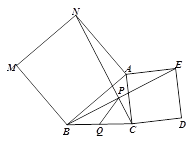
����Ŀ��̽������ͼ���ֱ��ԡ�ABC������AB��ACΪ��������������ABMN��������ACDE��CN��BE���ڵ�P. ��֤����ANC = ��ABE.
Ӧ�ã�Q���߶�BC���е㣬����PQ. ��BC = 6����PQ = ___________.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com