
【题目】在⊙O中,AB为⊙O的直径,AC是弦, ![]() ,
, ![]() .
.
(1)在图1中,P为直径BA延长线上的一点,当CP与⊙O相切时,求PO的长;
(2)如图2,一动点M从A点出发,在⊙O上按逆时针方向运动一周,当 ![]() 时,求半径OM所扫过的扇形的面积.
时,求半径OM所扫过的扇形的面积.
【答案】
(1)解:∵CP与⊙O相切,OC是半径.
∴CP⊥OC,
又∵∠OAC=∠AOC=60°,
∴∠P=90°-∠AOC=30°,
∴在Rt△POC中,CO= ![]() PO=4,
PO=4,
则PO=2CO=8
(2)解:如图,
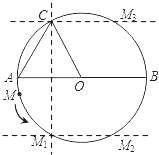
①作点C关于直径AB的对称点M1,连接AM1,OM1.
易得S△M1AO=S△CAO,∠AOM1=60°∴当点M运动到M1时,S△MAO=S△CAO,
此时点M经过的弧长为 ![]() ,
,
∴半径OM所扫过的扇形的面积= ![]() ;
;
②过点M1作M1M2∥AB交⊙O于点M2,连接AM2,OM2,易得S△M2AO=S△CAO.
∴∠AOM1=∠M1OM2=∠BOM2=60°
∴ ![]() 或
或 ![]() ,
,
∴当点M运动到M2时,S△MAO=S△CAO,此时点M经过的弧长为 ![]() ,
,
∴半径OM所扫过的扇形的面积= ![]() ×
× ![]() ×4=
×4= ![]() π;
π;
③过点C作CM3∥AB交⊙O于点M3,连接AM3,OM3,易得S△M3AO=S△CAO
∴∠BOM3=60°,
∴ ![]() =
= ![]() ×240或
×240或 ![]() =
= ![]() ×2=
×2= ![]()
∴当点M运动到M3时,S△MAO=S△CAO,此时点M经过的弧长为 ![]() ,
,
∴半径OM所扫过的扇形的面积= ![]() ×
× ![]() ×4=
×4= ![]() ;
;
④当点M运动到C时,M与C重合,S△MAO=S△CAO,
此时点M经过的弧长为 ![]() ×300°或
×300°或 ![]() π+
π+ ![]() =
= ![]()
∴半径OM所扫过的扇形的面积= ![]() ×
× ![]() ×4=
×4= ![]()
【解析】(1)根据CP与⊙O相切,得出CP⊥OC,根据题意易证△OAC是等边三角形,可求出∠P=30°,再根据直角三角形中,30°的直角边等于斜边的一半,求出OP的长。
(2)如图,当S△MAO=S△CAO时,动点M的位置有四种.①作点C关于直径AB的对称点M1,连接AM1,OM1,先证S△MAO=S△CAO,再求出点M经过的弧长,即可求出半径OM所扫过的扇形的面积;②过点M1作M1M2∥AB交 O于点M2,连接AM2,OM2,③过点C作CM3∥AB交 O于点M3,连接AM3,OM3;④当点M运动到C时,M与C重合,求得每种情况的OM转过的度数,再根据弧长公式求得点M经过的弧长,然后求出半径OM所扫过的扇形的面积。
【考点精析】解答此题的关键在于理解含30度角的直角三角形的相关知识,掌握在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半,以及对勾股定理的概念的理解,了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=4,AC=3,DE垂直平分AB,分别交AB、BC于点D、E,AP平分∠BAC,与DE的延长线交于点P.

(1)求PD的长度;
(2)连结PC,求PC的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数y = ![]() 的图象经过点A(1,-3),一次函数y =kx +b的图象经过点A与点C(0,-4),且与反比例函数的图象相交于另一点B.试确定点B的坐标.
的图象经过点A(1,-3),一次函数y =kx +b的图象经过点A与点C(0,-4),且与反比例函数的图象相交于另一点B.试确定点B的坐标.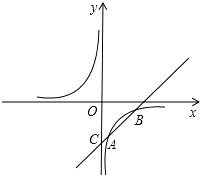
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1对应的函数表达式为y=2x-2,直线l1与x轴交于点D.直线l2:y=kx+b与x轴交于点A,且经过点B,直线l1,l2交于点C(m,2).
(1)求点D,点C的坐标;
(2)求直线l2对应的函数表达式;
(3)求△ADC的面积;
(4)利用函数图象写出关于x,y的二元一次方程组![]() 的解.
的解.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国南宋数学家杨辉用三角形解释二项和的乘方规律,称之为“杨辉三角”,这个三角形给出了(a+b)n(n═1,2,3,4,…)的展开式的系数规律(按n的次数由大到小的顺序):
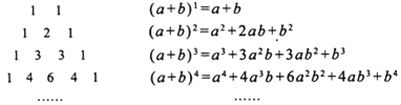
请依据上述规律,写出(x﹣2)2018展开式中含x2017项的系数是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】市场上甲种商品的采购价为60元/件,乙种商品的采购价为100元/件,某商店需要采购甲、乙两种商品共15件,且乙种商品的件数不少于甲种商品件数的2倍.设购买甲种商品![]() 件(
件(![]() >0),购买两种商品共花费
>0),购买两种商品共花费![]() 元.
元.
(1)求出![]() 与
与![]() 的函数关系式(写出自变量
的函数关系式(写出自变量![]() 的取值范围);
的取值范围);
(2)试利用函数的性质说明,当采购多少件甲种商品时,所需要的费用最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一副直角三角板如图①放置(其中![]() ,
,![]() ),
),![]() 、
、![]() 与直线
与直线![]() 重合,且三角板
重合,且三角板![]() ,三角板
,三角板![]() 均可以绕点
均可以绕点![]() 逆时针旋转.
逆时针旋转.
(l)直接写出![]() 等于多少度.
等于多少度.
(2)如图②,若三角板![]() 保持不动,三角板
保持不动,三角板![]() 绕点
绕点![]() 逆时针旋转,转速为
逆时针旋转,转速为![]() /秒,转动一周三角板
/秒,转动一周三角板![]() 就停止转动,在旋转的过程中,当旋转时间为多少时,有
就停止转动,在旋转的过程中,当旋转时间为多少时,有![]() 成立.
成立.
(3)如图③,在图①基础上,若三角板![]() 的边
的边![]() 从
从![]() .处开始绕点
.处开始绕点![]() 逆时针旋转,转速为
逆时针旋转,转速为![]() /秒,同时三角板
/秒,同时三角板![]() 的边
的边![]() 从
从![]() 处开始绕点
处开始绕点![]() 逆时针旋转,转速为
逆时针旋转,转速为![]() /秒,(当
/秒,(当![]() 转到与
转到与![]() 重合时,两三角板都停止转动),在旋转过程中,当
重合时,两三角板都停止转动),在旋转过程中,当![]() ,求旋转的时间是多少?
,求旋转的时间是多少?
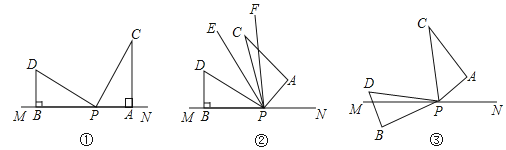
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com