练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，E是▱ABCD的边CD上一点，连接AE并延长交BC的延长线于点F，且AD=4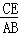，=，则CF的长为　 　．

    　


    2

    考点： 相似三角形的判定与性质；平行四边形的性质． 

    分析： 由四边形ABCD是平行四边形，即可得BC=AD=4，AB∥CD，继而可证得△FEC∽△FAB，由相似三角形的对应边成比例，即可求得答案．

    解答： 解：∵四边形ABCD是平行四边形，

    ∴BC=AD=4，AB∥CD，

    ∴△FEC∽△FAB，

    ∴==，

    ∴=，

    ∴CF=BC=×4=2．

    故答案为：2．

    点评： 此题考查了相似三角形的判定与性质以及平行四边形的性质．此题难度不大，注意掌握数形结合思想的应用．

    　

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


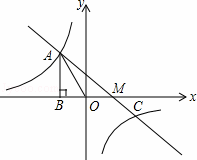
    已知反比例函数图象过第二象限内的点A（﹣2，m），作AB⊥x轴于点B，Rt△AOB面积为3．

    （1）求k和m的值；

    （2）若直线y=ax+b经过点A，并且经过反比例函数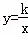的图象上另一点C（4，﹣）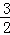

    ①求直线y=ax+b关系式；

    ②设直线y=ax+b与x轴交于M，求AM的长；

    ③根据图象写出使反比例函数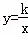值大于一次函数y=ax+b的值的x的取值范围．

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    关于x的一元二次方程（a﹣1）x2+x+（a2﹣1）=0的一个根是0，则a的值是　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    阅读材料：

    例：说明代数式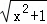+ 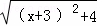的几何意义，并求它的最小值．

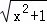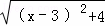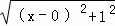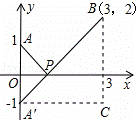
    解：+=+，如图，建立平面直角坐标系，点P（x，0）是x轴上一点，则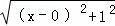可以看成点P与点A（0，1）的距离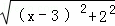，可以看成点P与点B（3，2）的距离，所以原代数式的值可以看成线段PA与PB长度之和，它的最小值就是PA+PB的最小值．

    设点A关于x轴的对称点为A′，则PA=PA′，因此，求PA+PB的最小值，只需求PA′+PB的最小值，而点A′、B间的直线段距离最短，所以PA′+PB的最小值为线段A′B的长度．为此，构造直角三角形A′CB，因为A′C=3，CB=3，所以A′B=3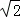，即原式的最小值为3．

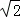    根据以上阅读材料，解答下列问题：

    （1）代数式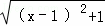+的值可以看成平面直角坐标系中点P（x，0）与点A（1，1）、点B（2，3）或（2，﹣3）的距离之和．（填写点B的坐标）

    （2）代数式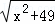+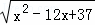的最小值．

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    二次函数y=x2+bx+c，若b+c=0，则它的图象一定过点（　　）

    　 A． （﹣1，﹣1） B． （1，﹣1） C． （﹣1，1） D． （1，1）

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    关于x的方程a（x+m）2+b=0的解是x1=﹣2，x2=1，（a，m，b均为常数，a≠0），则方程a（x+m+2）2+b=0的解是　                 　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知：如图，在△ABC中，D是BC边上的中点，且AD=AC，DE⊥BC，DE与AB相交于点E，EC与AD相交于点F．

    （1）求证：△ABC∽△FCD；

    （2）若S△FCD=5，BC=10，求DE的长．

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


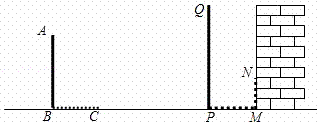
    在同一时刻两根木竿在太阳光下的影子如图所示，其中木竿AB=2m，它的影子BC=1.6m，木竿PQ的影子有一部分落在了墙上，PM=1.2m，MN=0.8m，则木竿PQ的长度为    m．

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，已知⊙O为△ABC的外接圆，CE是⊙O的直径，CD⊥AB，D为垂足，求证：∠ACD=∠BCE．

    　

    查看答案和解析>>

    同步练习册答案