
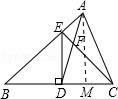
已知:如图,在△ABC中,D是BC边上的中点,且AD=AC,DE⊥BC,DE与AB相交于点E,EC与AD相交于点F.
(1)求证:△ABC∽△FCD;
(2)若S△FCD=5,BC=10,求DE的长.

考点: 相似三角形的判定与性质;三角形的面积.
专题: 几何综合题.
分析: (1)利用D是BC边上的中点,DE⊥BC可以得到∠EBC=∠ECB,而由AD=AC可以得到∠ADC=∠ACD,再利用相似三角形的判定,就可以证明题目结论;
(2)利用相似三角形的性质就可以求出三角形ABC的面积,然后利用面积公式就求出了DE的长.
解答: (1)证明:∵AD=AC,
∴∠ADC=∠ACD.
∵D是BC边上的中点,DE⊥BC,
∴EB=EC,
∴∠EBC=∠ECB.
∴△ABC∽△FCD;
(2)解:过A作AM⊥CD,垂足为M.
∵△ABC∽△FCD,BC=2CD,
∴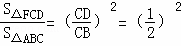 =
=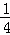 .
.
∵S△FCD=5,
∴S△ABC=20.
又∵S△ABC=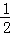 ×BC×AM,BC=10,
×BC×AM,BC=10,
∴AM=4.
又DM=CM=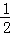 CD,DE∥AM,
CD,DE∥AM,
∴DE:AM=BD:BM=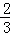 ,
,
∴DE=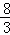 .
.
点评: 此题主要考查了相似三角形的性质与判定,也利用了三角形的面积公式求线段的长.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案科目:初中数学 来源: 题型:
钓鱼岛自古以来就是我国的神圣领土,为维护国家主权和海洋权利,我国海监和渔政部门对钓鱼岛 海域实现了常态化巡航管理.如图,某日在我国钓鱼岛附近海域有两艘自西向东航行的海监船A、B,B船在A船的正东方向,且两船保持20海里的距离,某一时刻两海监船同时测得在A的东北方向,B的北偏东15°方向有一我国渔政执法船C,求此时船C与船B的距离是多少.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
已知二次函数y=﹣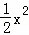 ﹣x+
﹣x+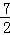 .
.
(1)用配方法把该二次函数的解析式化为y=a(x+m)2+k的形式;
(2)指出该二次函数图象的开口方向、顶点坐标和对称轴.
查看答案和解析>>
科目:初中数学 来源: 题型:
有一种可食用的野生菌,刚上市时,外商李经理以每千克30元的市场价格收购了这种野生菌1000千克存放入冷库中,据预测,该野生菌的市场价格将每天每千克上涨1元;但冷冻存放这批野生菌时每天需要支出各种费用合计310元,而且这种野生菌在冷库中最多保存140天,同时,平均每天有3千克的野生菌损坏导致不能出售.
(1)若存放x天后,将这批野生菌一次性出售,设这批野生菌的销售总额为P元,试求出P与x之间的函数关系式;
(2)李经理将这批野生菌存放多少天后一次性全部出售可以获得22500元的利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,一个半径为1的圆形纸片在边长为a(a≥2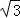 )的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片“不能接触到的部分”的面积是( )
)的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片“不能接触到的部分”的面积是( )
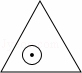
A. 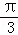 B.
B. 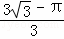
C. 3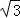 ﹣π D. 不能求出具体值
﹣π D. 不能求出具体值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com