
【题目】如图,△ABC是等边三角形,BD是AC边上的高,延长BC至E,使DB=DE.

(1)求∠BDE的度数;
(2)求证:△CED为等腰三角形.
【答案】(1)∠BDE=120°;(2)见解析
【解析】
(1)根据等边对等角得到∠E=∠DBE,根据等边三角形的性质得到∠ACB=∠ABC=60°,求得∠DBC=30°,根据三角形的内角和即可得到结论;
(2)根据三角形的外角的性质得到∠CDE=∠ACB﹣∠E=30°,根据等角对等边即可得到结论.
(1)∵DB=DE,∴∠E=∠DBE.
∵△ABC是等边三角形,∴∠ACB=∠ABC=60°.
∵△ABC是等边三角形,BD是高,∴∠DBC=30°,∴∠E=∠DBE=30°,∴∠BDE=180°-∠DBE-∠E=120°;
(2)∵∠ACB=60°,∠E=30°,∴∠CDE=∠ACB﹣∠E=30°,∴∠CDE=∠E,∴CD=CE,∴△CED是等腰三角形.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于![]() EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M。
EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M。

(1)若∠ACD=114°,求∠MAB的度数;
(2)若CN⊥AM,垂足为N,求证:△ACN≌△MCN。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】黑板上写有1,![]() ,
,![]() ,
,![]() ,…,
,…,![]() 共100个数字,每次操作先从黑板上的数中选取2个数a,b,然后删去a,b,并在黑板上写上数a+b+1,则经过_____次操作后,黑板上只剩下一个数,这个数是_____.
共100个数字,每次操作先从黑板上的数中选取2个数a,b,然后删去a,b,并在黑板上写上数a+b+1,则经过_____次操作后,黑板上只剩下一个数,这个数是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图象中所反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又 去早餐店吃早餐,然后散步走回家,其中 x 表示时间,y 表示张强离家的距离。根据图象提供的信息,以下四个说法错误的是( )
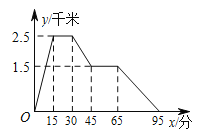
A. 体育场离张强家2.5千米 B. 张强在体育场锻炼了15分钟
C. 体育场离早餐店4千米 D. 张强从早餐店回家的平均速度是3千米/小时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴、y轴分别交于A、B两点,把△AOB绕点A顺时针旋转60°后得到△AO′B′,则点B'的坐标是( )
轴、y轴分别交于A、B两点,把△AOB绕点A顺时针旋转60°后得到△AO′B′,则点B'的坐标是( )

A. (4, ![]() ) B. (
) B. (![]() ,4) C. (
,4) C. (![]() ,3) D. (
,3) D. (![]() ,
, ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】结论:
①若a b c 0 ,且abc 0 ,则方程a bx c 0 的解是 x 1
②若a x 1 bx 1 有唯一的解,则a b;
③若b 2a ,则关于 x 的方程ax b 0a 0的解为 x ![]() ;
;
④若a b c 1,且a 0 ,则 x 1一定是方程ax b c 1的解.其中结论正确个数有( ).
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某园林部门决定利用现有的349盆甲种花卉和295盆乙种花卉搭配A. B两种园艺造型共50个,摆放在迎宾大道两侧。已知搭配一个A种造型需甲种花卉8盆,乙种花卉4盆;搭配一个B种造型需甲种花卉5盆,乙种花卉9盆。
(1)某校九年级某班课外活动小组承接了这个园艺造型搭配方案的设计,问符合题意的搭配方案有几种?请你帮助设计出来;
(2)若搭配一个A种造型的成本是200元,搭配一个B种造型的成本是360元,试说明(1)中哪种方案成本最低,最低成本是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com