
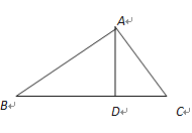
【题目】如图,△ABC中,∠BAC=90°,AD⊥BC,垂足为D.
(1)求作∠ABC的平分线,分别交AD,AC于E,F两点;(要求:尺规作图,保留作图痕迹,不写作法)
(2)证明:AE=AF.
【答案】(1)见解析;(2)证明见解析.
【解析】
(1)利用基本作图(作已知角的角平分线)作BF平分∠ABC即可;
(2)分析题意,首先根据角平分线的作法作出∠ABC的角平分线,并标注点E、F即可;根据直角三角形的性质,可得出∠BED+∠EBD=90°,∠AFE+∠ABF=90°,进而得出∠BED=∠AFE; 接下来根据对顶角相等,可得出∠AEF=∠AFE,据此可得到结论.
解:(1)如图所示,射线BF即为所求
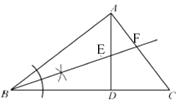
(2)证明:∵AD⊥BC
∴∠ADB=90°
∴∠BED+∠EBD=90°
∵∠BAC=90°
∴∠AFE+∠ABF=90°
∵∠EBD=∠ABF
∴∠AFE=∠BED,
∵∠AEF=∠BED
∴∠AEF=∠AFE
∴AE=AF


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】为了帮助市内一名患“白血病”的中学生,东营市某学校数学社团15名同学积极捐款,捐款情况如下表所示,下列说法正确的是( )
捐款数额 | 10 | 20 | 30 | 50 | 100 |
人数 | 2 | 4 | 5 | 3 | 1 |
A. 众数是100 B. 中位数是30 C. 极差是20 D. 平均数是30
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学的高中部在A校区,初中部在B校区,学校学生会计划在3月12日植树节当天安排部分学生到郊区公园参加植树活动.已知A校区的每位高中学生往返车费是6元,B校区的每位初中学生往返的车费是10元,要求初、高中均有学生参加,且参加活动的初中学生比参加活动的高中学生多4人,本次活动的往返车费总和不超过210元,求初、高中最多各有多少学生参加.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂接受了20天内生产1200台GH型电子产品的总任务.已知每台GH型产品由4个G型装置和3个H型装置配套组成.工厂现有80名工人,每个工人每天能加工6个G型装置或3个H型装置.工厂将所有工人分成两组同时开始加工,每组分别加工一种装置,并要求每天加工的G、H型装置数量正好全部配套组成GH型产品.
(1)按照这样的生产方式,工厂每天能配套组成多少套GH型电子产品?请列出二元一次方程组解答此问题.
(2)为了在规定期限内完成总任务,工厂决定补充一些新工人,这些新工人只能独立进行G型装置的加工,且每人每天只能加工4个G型装置.1.设原来每天安排x名工人生产G型装置,后来补充m名新工人,求x的值(用含m的代数式表示)2.请问至少需要补充多少名新工人才能在规定期内完成总任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=108°,EF、MN分别是AB、AC的垂直平分线,点E、N在BC上,则∠EAN等于( )
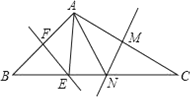
A. 72°B. 54°C. 36°D. 18°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】郴州市正在创建“全国文明城市”,某校拟举办“创文知识”抢答赛,欲购买A、B两种奖品以鼓励抢答者.如果购买A种20件,B种15件,共需380元;如果购买A种15件,B种10件,共需280元.
(1)A、B两种奖品每件各多少元?
(2)现要购买A、B两种奖品共100件,总费用不超过900元,那么A种奖品最多购买多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,过点O作两条射线OM、ON,且∠AOM=∠CON=90°

(1)若OC平分∠AOM,求∠AOD的度数.
(2)若∠1=![]() ∠BOC,求∠AOC和∠MOD.
∠BOC,求∠AOC和∠MOD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班对道德与法治,历史,地理三门程的选考情况进行调研,数据如下:
科目 | 道德与法治 | 历史 | 地理 |
选考人数(人) | 19 | 13 | 18 |
其中道德与法治,历史两门课程都选了的有3人,历史,地理两门课程都选了的有4人,该班至多有多少学生( )
A.41B.42C.43D.44
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学活动课上,小明提出这样一个问题:∠B=∠C=90°,E是BC的中点,DE平分∠ADC,∠CDE=55°.如图,则∠EAB的度数为_________
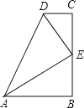
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com