

·ЦОц ЈЁ1Ј©УЙМвТвҝЙЦӘөгPҙУAөҪCРиТӘ2ГлЈ¬ҙУCөҪBРиТӘ2ГлЈ¬ҙУ¶шҝЙЗуөГt=5КұЈ¬өгPФЛ¶ҜөДВ·іМЈ¬өгPУлөгЦШәПЈ¬ФтөгPФЛ¶ҜөДҫаАл-өгEФЛ¶ҜөДҫаАл=ACЈ¬ҙУ¶шҝЙЗуөГөгt=3Ј»
ЈЁ2Ј©УЙlЎОACҝЙЦӘЎПA=ЎПEFHЈ¬№КtanЎПEFH=$\frac{4}{3}$Ј¬УЙПаЛЖИэҪЗРОөДРФЦКҝЙЦӘ$\frac{PC}{EC}=\frac{3}{4}$»т$\frac{PC}{EC}=\frac{4}{3}$Ј¬ҙУ¶шЗуөГt=$\frac{3}{2}$»тt=$\frac{54}{43}$Ј¬И»әуУЙtөДЦөҝЙЗуөГCEөДіӨЈ¬ҙУ¶шҝЙЗуөГBEөДіӨЈ¬ЧоәуФЪRtЎчEHBЦРУЙEH=EBЎБ$\frac{3}{5}$ҝЙЗуөГEHөДіӨЈ»
ЈЁ3Ј©өұөгPФЪACЙПКұЈ¬Б¬ҪбPQЈ®УЙБвРОөДРФЦКҝЙЦӘPQҙ№ЦұЖҪ·ЦEFЈ¬ҙУ¶шөГөҪEF=2CPЈ¬УЙМвТвҝЙЦӘPC=6-3tЈ¬ФЪЎчEFBЦРЈ¬tanЎПB=$\frac{3}{4}$Ј¬УЪКЗҝЙЗуөГEF=$\frac{3}{4}$BE=$\frac{3}{4}ЎБЈЁ8-\frac{4}{3}tЈ©$Ј¬ҝЙЗуөГt=$\frac{6}{5}$Јј2Ј¬·ыәПМвТвЈ»өұөгPФЪCBЙПФЛ¶ҜКұЈ¬өгPЎўQЎўEФЪТ»МхЦұПЯЙПЈ¬өгPЎўQЎўEЎўFІ»ДЬ№№іЙЛДұЯРОЈ»өұөгPФЪBAЙПФЛ¶ҜКұЈ¬УЙБвРОөДРФЦКҝЙЦӘPE=PFЈ¬И»әуёщҫЭөИҪЗөДУаҪЗПаөИҝЙЦӘPB=PEЈ¬№КҙЛҝЙЦӘBF=2BPЈ¬УЙМвТвҝЙЦӘPB=5ЈЁt-4Ј©ФЪRtЎчEFBЦРЈ¬FB=$\frac{5}{4}EB$=$\frac{5}{4}$ЈЁ8-$\frac{4}{3}t$Ј©Ј¬№КҙЛҝЙҪвөГt=$\frac{30}{7}$Ј®
Ҫвҙр ҪвЈәЈЁ1Ј©ЎЯAC=6Ј¬өгPФЪACЙПФЛ¶ҜөДЛЩ¶ИОӘГҝГл3ёцөҘО»Ј¬
Ўа6ЎВ3=2ГлЈ®
ЎЯBC=8Ј¬өгPФЪCBЙПФЛ¶ҜөДЛЩ¶ИОӘГҝГл4ёцөҘО»Ј¬
Ўа8ЎВ4=2ГлЈ®
өұt=5ГлКұЈ¬өгPФЛ¶ҜөДВ·іМ=6+8+5=19Ј®
өұФЛ¶ҜКұјдОӘtГлКұЈ¬өгPУлөгEЦШәПЈ®
ёщҫЭМвТвөГЈә4ЈЁt-2Ј©=$\frac{4}{3}t$Ј®
ҪвөГЈәt=3Ј®
№Кҙр°ёОӘЈә19Ј»3Ј®
ЈЁ2Ј©ЎЯlЎОACЈ¬
ЎаЎПA=ЎПEFHЈ®
ЎаtanЎПEFH=tanЎПA=$\frac{4}{3}$Ј®
ЎЯЎчCPEЎЧEFHЈ¬
Ўа$\frac{PC}{EC}=\frac{3}{4}$»т$\frac{PC}{EC}=\frac{4}{3}$
ЎЯCP=6-3tЈ¬CE=$\frac{4}{3}$tЈ¬
Ўа$\frac{6-3t}{\frac{4}{3}t}$=$\frac{3}{4}$»т$\frac{6-3t}{\frac{4}{3}t}$=$\frac{4}{3}$Ј®
ҪвөГЈәt=$\frac{3}{2}$»тt=$\frac{54}{43}$Ј®
ЎЯөұt=$\frac{3}{2}$КұЈ¬CE=$\frac{4}{3}t$=$\frac{4}{3}ЎБ\frac{3}{2}$=2Ј®
ЎаBE=BC-EC=8-2=6Ј®
ФЪRtЎчEHBЦРЈ¬EH=EBЎБ$\frac{3}{5}$=6ЎБ$\frac{3}{5}$=$\frac{18}{5}$Ј®
ЎаEH=$\frac{18}{5}$Ј®
ЎЯөұt=$\frac{54}{43}$КұЈ¬EC=$\frac{4}{3}t$=$\frac{4}{3}ЎБ\frac{54}{43}$=$\frac{72}{43}$Ј¬
ЎаEB=8-$\frac{72}{43}$=$\frac{272}{43}$Ј®
ФЪRtЎчEHBЦРЈ¬EH=EBЎБ$\frac{3}{5}$=$\frac{72}{43}$ЎБ$\frac{3}{5}$=$\frac{816}{215}$Ј®
ЎаEH=$\frac{816}{215}$Ј®
ЈЁ3Ј©ИзНј1ЛщКҫЈәөұөгPФЪACЙПКұЈ¬Б¬ҪбPQЈ®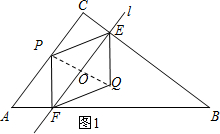
ЎЯЛДұЯРОPEQFОӘБвРОЈ¬
ЎаPQҙ№ЦұЖҪ·ЦEFЈ®
ЎаЎПEOP=90ЎгЈ®
ЎЯlЎОACЈ¬ЎПC=90ЎгЈ¬
ЎаЎПCEO=90Ўг
ЎЯЎПC=ЎПCEO=ЎПEOP=90ЎгЈ¬
ЎаЛДұЯРОCEQPОӘҫШРОЈ®
ЎаPC=EOЈ®
ЎаEF=2CPЈ®
ЎЯCE=$\frac{4}{3}t$Ј¬
ЎаEB=8-$\frac{4}{3}t$Ј®
ЎЯФЪЎчEFBЦРЈ¬tanЎПB=$\frac{3}{4}$Ј¬
ЎаEF=$\frac{3}{4}$BE=$\frac{3}{4}ЎБЈЁ8-\frac{4}{3}tЈ©$Ј®
ЎЯAP=3tЈ¬AC=6Ј¬
ЎаPC=6-3tЈ®
Ўа$\frac{3}{4}$ЈЁ8-$\frac{4}{3}$tЈ©=2ЈЁ6-3tЈ©Ј®
ҪвөГt=$\frac{6}{5}$Јј2Ј¬·ыәПМвТвЈ®
өұөг PФЪCBЙПФЛ¶ҜКұЈ¬өгPЎўQЎўEФЪТ»МхЦұПЯЙПЈ¬өгPЎўQЎўEЎўFІ»ДЬ№№іЙЛДұЯРОЈ®
ИзНј2ЛщКҫЈәөұөг PФЪBAЙПФЛ¶ҜКұЈ®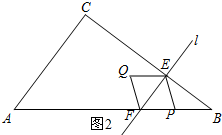
ЎЯЛДұЯРОPEQFОӘБвРОЈ¬
ЎаPE=PFЈ®
ЎаЎПPFE=ЎПPEFЈ®
ЎЯЎПEFP+ЎПB=90ЎгЈ¬ЎПFEP+ЎПPEB=90ЎгЈ¬
ЎаЎПPEB=ЎПPBEЈ®
ЎаPB=PEЈ®
ЎаBF=2BPЈ®
ЎЯCE=$\frac{4}{3}t$Ј¬BC=8Ј¬
ЎаBE=8-$\frac{4}{3}t$Ј®
ФЪRtЎчEFBЦРЈ¬FB=$\frac{5}{4}EB$=$\frac{5}{4}$ЈЁ8-$\frac{4}{3}t$Ј©Ј®
УЙМвТвҝЙЦӘЈәPB=5ЈЁt-4Ј©Ј®
Ўа$\frac{5}{4}$ЈЁ8-$\frac{4}{3}$tЈ©=2ЎБ5ЈЁt-4Ј©Ј¬
ҪвөГt=$\frac{30}{7}$Ј®
ЧЫЙПЛщКцЈ¬өұt=$\frac{6}{5}$Гл»тt=$\frac{30}{7}$ГлКұЈ¬ЛДұЯРОPEQFОӘБвРОЈ®
өгЖА ұҫМвЦчТӘҝјІйөДКЗТ»ҙОәҜКэөДЧЫәПУҰУГЎўПаЛЖИэҪЗРОөДРФЦКЎўЦб¶ФіЖНјРОөДРФЦКЎўБвРОөДРФЦКЎўИсҪЗИэҪЗәҜКэөД¶ЁТеЈ¬ТАҫЭөгPФЛ¶ҜөДЛЩ¶ИТФј°МШКвИсҪЗИэҪЗәҜКэЦөұнКҫПа№ШПЯ¶ОөДіӨ¶ИКЗҪвМвөД№ШјьЈ®


 ФД¶БҝміөПөБРҙр°ё
ФД¶БҝміөПөБРҙр°ё
| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәМоҝХМв
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәСЎФсМв
| AЈ® | ЈЁ-4Ј¬-1Ј© | BЈ® | ЈЁ1Ј¬-4Ј© | CЈ® | ЈЁ-5Ј¬1Ј© | DЈ® | ЈЁ-1Ј¬4Ј© |
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәҪвҙрМв

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәҪвҙрМв
 ТСЦӘ¶аПоКҪm5n2-1ЦРЈ¬ә¬ЧЦДёөДПоөДПөКэОӘbЈ¬¶аПоКҪөДҙОКэОӘcЈ¬іЈКэПоОӘaЈ¬Зл»ШҙрОКМвЈ®
ТСЦӘ¶аПоКҪm5n2-1ЦРЈ¬ә¬ЧЦДёөДПоөДПөКэОӘbЈ¬¶аПоКҪөДҙОКэОӘcЈ¬іЈКэПоОӘaЈ¬Зл»ШҙрОКМвЈ®Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәСЎФсМв
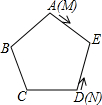 ИзНјЈ¬MЎўNКЗХэОеұЯРОABCDEёчұЯЙПөДБҪёц¶ҜөгЈ¬ИфЛьГЗ·ЦұрҙУ¶ҘөгAЎўDіц·ўЈ¬Н¬КұСШХэОе·ҪРОөДұЯТЖ¶ҜЈ¬MөгТФЛіКұХл·ҪПтТЖ¶ҜЈ¬NөгТФДжКұХл·ҪПтТЖ¶ҜЈ¬јЩЙиөгMөДЛЩ¶ИКЗөгNөДЛЩ¶ИөД5ұ¶Ј¬ФтЛьГЗөЪ2014ҙОПаУцФЪЈЁЎЎЎЎЈ©ұЯЙПЈ®
ИзНјЈ¬MЎўNКЗХэОеұЯРОABCDEёчұЯЙПөДБҪёц¶ҜөгЈ¬ИфЛьГЗ·ЦұрҙУ¶ҘөгAЎўDіц·ўЈ¬Н¬КұСШХэОе·ҪРОөДұЯТЖ¶ҜЈ¬MөгТФЛіКұХл·ҪПтТЖ¶ҜЈ¬NөгТФДжКұХл·ҪПтТЖ¶ҜЈ¬јЩЙиөгMөДЛЩ¶ИКЗөгNөДЛЩ¶ИөД5ұ¶Ј¬ФтЛьГЗөЪ2014ҙОПаУцФЪЈЁЎЎЎЎЈ©ұЯЙПЈ®| AЈ® | AE | BЈ® | ED | CЈ® | CD | DЈ® | AB |
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәСЎФсМв
| AЈ® | x2=1 | BЈ® | xЈЁx-1Ј©=xЈЁx-2Ј© | CЈ® | x2+2=0 | DЈ® | xЈЁx-1Ј©=x |
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәСЎФсМв
| AЈ® | -$\frac{4}{9}$ | BЈ® | 1 | CЈ® | $\frac{4}{9}$ | DЈ® | 1»т$\frac{4}{9}$ |
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәМоҝХМв
Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com