
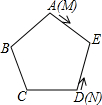
 如图,M、N是正五边形ABCDE各边上的两个动点,若它们分别从顶点A、D出发,同时沿正五方形的边移动,M点以顺时针方向移动,N点以逆时针方向移动,假设点M的速度是点N的速度的5倍,则它们第2014次相遇在( )边上.
如图,M、N是正五边形ABCDE各边上的两个动点,若它们分别从顶点A、D出发,同时沿正五方形的边移动,M点以顺时针方向移动,N点以逆时针方向移动,假设点M的速度是点N的速度的5倍,则它们第2014次相遇在( )边上.| A. | AE | B. | ED | C. | CD | D. | AB |
分析 设每边长为1,刚开始M、N之间的距离是2,M的速度是N的5倍,所以M走它们距离的$\frac{5}{6}$,也就是2×$\frac{5}{6}$=$\frac{5}{3}$,为整个图形周长的$\frac{1}{3}$,也就是第一次相遇在DE上,距离D$\frac{1}{3}$处,以此类推,第二次点N走的路程为5×$\frac{1}{6}$=$\frac{5}{6}$,此时点N走的路程为$\frac{1}{3}$+$\frac{5}{6}$=$\frac{7}{6}$,相遇在AE上距离E$\frac{1}{6}$处,第三次点N走的路程为$\frac{1}{3}$+$\frac{5}{6}$+$\frac{5}{6}$=2,相遇在点A,第四次点N走的路程为$\frac{1}{3}$+$\frac{5}{6}$+$\frac{5}{6}$+$\frac{5}{6}$=2$\frac{5}{6}$,相遇在AB上距离B$\frac{1}{6}$处,第五次相遇点N走的路程为$\frac{1}{3}$+$\frac{5}{6}$×4=$\frac{11}{3}$,相遇在在BC上距离C$\frac{1}{3}$处,第六次点N走的路程为$\frac{1}{3}$+$\frac{5}{6}$×5=$\frac{9}{2}$,相遇在相遇在CD中点处,第七次点N走的路程为$\frac{1}{3}$+$\frac{5}{6}$×6=5$\frac{1}{3}$,相遇在相遇在第一次相遇处,所以6次一个循环从而不难求得它们第2014次相遇位置.
解答 解:设每边长为1,刚开始M、N之间的距离是2,M的速度是N的5倍,所以M走它们距离的$\frac{5}{6}$,也就是2×$\frac{5}{6}$=$\frac{5}{3}$,为整个图形周长的$\frac{1}{3}$,也就是第一次相遇在DE上,距离D$\frac{1}{3}$处,以此类推,第二次点N走的路程为5×$\frac{1}{6}$=$\frac{5}{6}$,此时点N走的路程为$\frac{1}{3}$+$\frac{5}{6}$=$\frac{7}{6}$,相遇在AE上距离E$\frac{1}{6}$处,第三次点N走的路程为$\frac{1}{3}$+$\frac{5}{6}$+$\frac{5}{6}$=2,相遇在点A,第四次点N走的路程为$\frac{1}{3}$+$\frac{5}{6}$+$\frac{5}{6}$+$\frac{5}{6}$=2$\frac{5}{6}$,相遇在AB上距离B$\frac{1}{6}$处,第五次相遇点N走的路程为$\frac{1}{3}$+$\frac{5}{6}$×4=$\frac{11}{3}$,相遇在在BC上距离C$\frac{1}{3}$处,第六次点N走的路程为$\frac{1}{3}$+$\frac{5}{6}$×5=$\frac{9}{2}$,相遇在相遇在CD中点处,第七次点N走的路程为$\frac{1}{3}$+$\frac{5}{6}$×6=5$\frac{1}{3}$,相遇在相遇在第一次相遇处,所以6次一个循环;
2014÷6=335…4,
第2014次相遇点与第四次相遇在AB上.
故选:D.
点评 此题考查图形的变化规律,找出点在边上循环周期,得出6次一个循环是解决问题的关键.


 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5cm,9cm,12cm | B. | 7cm,12cm,13cm | C. | 30cm,40cm,50cm | D. | 3cm,4cm,6cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com