
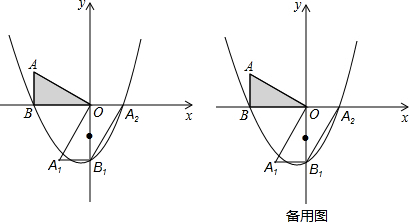
ЗжЮі ЃЈ1ЃЉЪзЯШИљОна§зЊЕФаджЪШЗЖЈЕуBЁЂB1ЁЂA2Ш§ЕуЕФзјБъЃЌШЛКѓРћгУД§ЖЈЯЕЪ§ЗЈЧѓЕУХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЧѓГіЁїPBB1ЕФУцЛ§БэДяЪНЃЌетЪЧвЛИіЙигкPЕуКсзјБъЕФЖўДЮКЏЪ§ЃЌРћгУЖўДЮКЏЪ§ЧѓМЋжЕЕФЗНЗЈЧѓГіЁїPBB1УцЛ§ЕФзюДѓжЕЃЛжЕЕУзЂвтЕФЪЧЧѓЁїPBB1УцЛ§ЕФЗНЗЈЃЌШчЭМ1ЫљЪОЃЛ
ЃЈ3ЃЉИљОнД§ЖЈЯЕЪ§ЗЈЃЌПЩЕУBB1ЕФНтЮіЪНЃЌЙ§BЕуДЙжБBB1ЕФНтЮіЪНЃЌЙ§B1ЕуДЙжБBB1ЕФНтЮіЪНЃЌИљОнНтЗНГЬзщЃЌПЩЕУДЙжБBB1ЕФжБЯпгыХзЮяЯпЕФНЛЕузјБъЃЌИљОнЕкШ§ЯѓЯоФкЕуЕФКсзјБъаЁгкСуЃЌзнзјБъаЁгкСуЃЌПЩЕУД№АИЃЎ
НтД№ НтЃКЃЈ1ЃЉЁпABЁЭxжсЃЌAЃЈ-4ЃЌ3ЃЉЃЌOB=4ЃЌ
ЁрBЃЈ-4ЃЌ0ЃЉЃЌB1ЃЈ0ЃЌ-4ЃЉЃЌA2ЃЈ3ЃЌ0ЃЉЃЎ
ЁпХзЮяЯпy=ax2+bx+cЃЈaЁй0ЃЉОЙ§ЕуBЁЂB1ЁЂA2ЃЌ
Ёр$\left\{\begin{array}{l}{16a-4b+c=0}\\{c=-4}\\{9a+3b+c=0}\end{array}\right.$ЃЌ
НтЕУ$\left\{\begin{array}{l}{a=\frac{1}{3}}\\{b=\frac{1}{3}}\\{c=-4}\end{array}\right.$ЃЎ
ЁрХзЮяЯпЕФНтЮіЪНЮЊЃКy=$\frac{1}{3}$x2+$\frac{1}{3}$x-4ЃЎ
ЃЈ2ЃЉЕуPЪЧЕкШ§ЯѓЯоФкХзЮяЯпy=$\frac{1}{3}$x2+$\frac{1}{3}$x-4ЩЯЕФвЛЕуЃЌ
ШчЭМ1ЃЌЕуPзїPCЁЭxжсгкЕуCЃЎ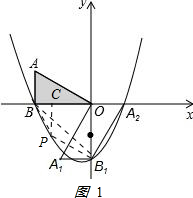
ЩшЕуPЕФзјБъЮЊЃЈmЃЌnЃЉЃЌдђmЃМ0ЃЌnЃМ0ЃЌn=$\frac{1}{3}$m2+$\frac{1}{3}$m-4ЃЎ
гкЪЧPC=|n|=-n=-$\frac{1}{3}$m2-$\frac{1}{3}$m+4ЃЌOC=|m|=-mЃЌBC=OB-OC=|-4|-|m|=4+mЃЎ
SЁїPBB1=SЁїPBC+SЬнаЮPB1OC-SЁїOBB1
=$\frac{1}{2}$ЁСBCЁСPC+$\frac{1}{2}$ЁСЃЈPC+OB1ЃЉЁСOC-$\frac{1}{2}$ЁСOBЁСOB1
=$\frac{1}{2}$ЁСЃЈ4+mЃЉЁСЃЈ-$\frac{1}{3}$m2-$\frac{1}{3}$m+4ЃЉ+$\frac{1}{2}$ЁС[ЃЈ-$\frac{1}{3}$m2-$\frac{1}{3}$m+4ЃЉ+4]ЁСЃЈ-mЃЉ-$\frac{1}{2}$ЁС4ЁС4
=-$\frac{2}{3}$m2-$\frac{8}{3}$m
=-$\frac{2}{3}$ЃЈm+2ЃЉ2+$\frac{8}{3}$ЃЌ
ЕБm=-2ЪБЃЌЁїPBB1ЕФУцЛ§зюДѓЃЌетЪБЃЌn=-$\frac{10}{3}$ЃЌМДЕуPЃЈ-2ЃЌ-$\frac{10}{3}$ЃЉЃЛ
ЃЈ3ЃЉдкЕкШ§ЯѓЯоФкЃЌХзЮяЯпЩЯВЛДцдкЕуQЃЌЪЙЕУЁїQBB1ЮЊвдBB1ЮЊжБНЧБпЕФжБНЧШ§НЧаЮЃЌРэгЩШчЯТЃК
BB1ЕФНтЮіЪНЮЊy=-x-4ЃЌ
Й§BЕуДЙжБBB1ЕФНтЮіЪНЮЊy=x+4ЃЌ
Й§B1ЕуДЙжБBB1ЕФНтЮіЪНЮЊy=x-4ЃЌ
ЂйСЊСЂХзЮяЯпгыЙ§BЕуДЙжБBB1ЕФжБЯпЃЌЕУ
$\left\{\begin{array}{l}{y=-\frac{1}{3}{x}^{2}-\frac{1}{3}x+4}\\{y=x+4}\end{array}\right.$ЃЌ
ЯћдЊЛЏМђЃЌЕУx2-2x-24=0ЃЌ
НтЕУx1=-4ЃЌx2=6ЃЌ
ЕБx1=-4ЪБЃЌy=0ЃЌМДЕуЕФзјБъЪЧЃЈ-4ЃЌ0ЃЉЃЌ
ЕуЃЈ-4ЃЌ0ЃЉВЛдкЕкШ§ЯѓЯоЃЌ
ЕБx=6ЪБЃЌy=6+4=10ЃЌМДНЛЕузјБъЃЈ6ЃЌ10ЃЉЃЌ
ЕуЃЈ6ЃЌ10ЃЉВЛдкЕкШ§ЯѓЯоЃЛ
ЂкСЊСЂХзЮяЯпгыЙ§B1ЕуДЙжБBB1ЕФжБЯпЃЌЕУ
$\left\{\begin{array}{l}{y=-\frac{1}{3}{x}^{2}-\frac{1}{3}x+4}\\{y=x-4}\end{array}\right.$ЃЌ
ЯћдЊЛЏМђЃЌЕУx2-2x=0ЃЌ
НтЕУx1=0ЃЌx2=2ЃЌ
ЕБx1=-0ЪБЃЌy=-4ЃЌМДЕуЕФзјБъЪЧЃЈ0ЃЌ-4ЃЉЃЌ
ЕуЃЈ0ЃЌ-4ЃЉВЛдкЕкШ§ЯѓЯоЃЌ
ЕБx=2ЪБЃЌy=2-4=-2ЃЌМДНЛЕузјБъЃЈ2ЃЌ-4ЃЉЃЌ
ЕуЃЈ2ЃЌ-4ЃЉВЛдкЕкШ§ЯѓЯоЃЛ
злЩЯЫљЪіЃЌДЙжБBB1ЕФжБЯпгыХзЮяЯпЕФНЛЕуЖМВЛдкЕкШ§ЯѓЯоЃЌ
дкЕкШ§ЯѓЯоФкЃЌХзЮяЯпЩЯВЛДцдкЕуQЃЌЪЙЕУЁїQBB1ЮЊвдBB1ЮЊжБНЧБпЕФжБНЧШ§НЧаЮЃЎ
ЕуЦР БОЬтзлКЯПМВщСЫД§ЖЈЯЕЪ§ЗЈЧѓХзЮяЯпНтЮіЪНЁЂЖўДЮКЏЪ§ЭМЯѓЩЯЕуЕФзјБъЬиеїЁЂвЛдЊЖўДЮЗНГЬЁЂа§зЊгызјБъБфЛЏЁЂЭМаЮУцЛ§ЧѓЗЈЁЂЙДЙЩЖЈРэЕШживЊжЊЪЖЕуЃЎЕкЃЈ2ЃЉЮЪЦ№ГаЩЯЦєЯТЕФзїгУЃЌЪЧБОЬтЕФФбЕугыКЫаФЃЌЦфжаЕФвЊЕуЪЧзјБъЦНУцФкЭМаЮУцЛ§ЕФЧѓНтЗНЗЈЃЌетжжЗНЗЈЪЧбЙжсЬтжаГЃМћЕФвЛжжНтЬтЗНЗЈЃЌЭЌбЇУЧашвЊШЯецеЦЮеЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | ЃЈ-4ЃЌ-1ЃЉ | BЃЎ | ЃЈ1ЃЌ-4ЃЉ | CЃЎ | ЃЈ-5ЃЌ1ЃЉ | DЃЎ | ЃЈ-1ЃЌ4ЃЉ |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
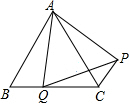 ШчЭМЃЌЕуQЪЧЕШБпЁїABCЕФБпBCЩЯвЛЕуЃЌвдAQЮЊБпзїЕШБпЁїAQPЃЌЧѓжЄЃКPCЁЮABЃЎ
ШчЭМЃЌЕуQЪЧЕШБпЁїABCЕФБпBCЩЯвЛЕуЃЌвдAQЮЊБпзїЕШБпЁїAQPЃЌЧѓжЄЃКPCЁЮABЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
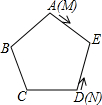 ШчЭМЃЌMЁЂNЪЧе§ЮхБпаЮABCDEИїБпЩЯЕФСНИіЖЏЕуЃЌШєЫќУЧЗжБ№ДгЖЅЕуAЁЂDГіЗЂЃЌЭЌЪБбие§ЮхЗНаЮЕФБпвЦЖЏЃЌMЕувдЫГЪБеыЗНЯђвЦЖЏЃЌNЕувдФцЪБеыЗНЯђвЦЖЏЃЌМйЩшЕуMЕФЫйЖШЪЧЕуNЕФЫйЖШЕФ5БЖЃЌдђЫќУЧЕк2014ДЮЯргідкЃЈЁЁЁЁЃЉБпЩЯЃЎ
ШчЭМЃЌMЁЂNЪЧе§ЮхБпаЮABCDEИїБпЩЯЕФСНИіЖЏЕуЃЌШєЫќУЧЗжБ№ДгЖЅЕуAЁЂDГіЗЂЃЌЭЌЪБбие§ЮхЗНаЮЕФБпвЦЖЏЃЌMЕувдЫГЪБеыЗНЯђвЦЖЏЃЌNЕувдФцЪБеыЗНЯђвЦЖЏЃЌМйЩшЕуMЕФЫйЖШЪЧЕуNЕФЫйЖШЕФ5БЖЃЌдђЫќУЧЕк2014ДЮЯргідкЃЈЁЁЁЁЃЉБпЩЯЃЎ| AЃЎ | AE | BЃЎ | ED | CЃЎ | CD | DЃЎ | AB |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
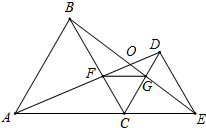 ШчЭМЃЌЕуAЃЌCЃЌEдквЛЬѕжБЯпЩЯЃЌвбжЊABCКЭЁїEDCЖМЪЧЕШБпШ§НЧаЮЃЌADЃЌBEЯрНЛгкЕуOЃЌADЃЌBCЯрНЛгкЕуFЃЌCDЃЌBEЯрНЛгкЕуGЃЎСЌНгFGКЭOCЃЎ
ШчЭМЃЌЕуAЃЌCЃЌEдквЛЬѕжБЯпЩЯЃЌвбжЊABCКЭЁїEDCЖМЪЧЕШБпШ§НЧаЮЃЌADЃЌBEЯрНЛгкЕуOЃЌADЃЌBCЯрНЛгкЕуFЃЌCDЃЌBEЯрНЛгкЕуGЃЎСЌНгFGКЭOCЃЎВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com