
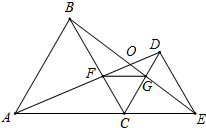
 如图,点A,C,E在一条直线上,已知ABC和△EDC都是等边三角形,AD,BE相交于点O,AD,BC相交于点F,CD,BE相交于点G.连接FG和OC.
如图,点A,C,E在一条直线上,已知ABC和△EDC都是等边三角形,AD,BE相交于点O,AD,BC相交于点F,CD,BE相交于点G.连接FG和OC.分析 (1)根据等边三角形性质得出AC=BC,CE=CD,∠ACB=∠ECD=60°,求出∠BCE=∠ACD,根据SAS推出两三角形全等即可;
(2)连接OC,根据三角形的内角和得到∠AOB=60°,于是得到∠ODC+∠DEO=60°,求得∠ODC=∠CEO,同理∠OCD=∠DEO,于是得到∠COE=60°,同理∠AOC=60°,求得∠AOC=∠EOC;故③正确;根据三角形的内角和和已知条件得到∠DFG+∠FDG=60°,于是得到∠FGD=∠ACD=120°,证得PQ∥AE,故②正确;根据平行线的性质得到∠CFG=∠ACB=60°,由∠FCG=60°,于是得到△CFG为等边三角形,得到CF=CG,推出△ACF≌△BCG,根据全等三角形的性质得到AF=BG;故①正确;
(3)在OE上截取OH=OC,推出OC=OH=CH,根据等边三角形的性质∠OCH=60°,于是得到∠OCG=∠HCE,证得△OCD≌△HCE,根据全等三角形的性质得到HE=OD,即可得到结论.
解答 证明:(1)∵△ABC和△CDE都是等边三角形,
∴AC=BC,CE=CD,∠ACB=∠ECD=60°,
∴∠ACB+∠ACE=∠ECD+∠ACE,
即∠BCE=∠ACD,
在△BCE和△ACD中,
$\left\{\begin{array}{l}{BC=AC}\\{∠BCE=∠ACD}\\{CE=CD}\end{array}\right.$,
∴△BCE≌△ACD(SAS),
∴AD=BE;
(2)正确的有①②③,
证明:连接OC,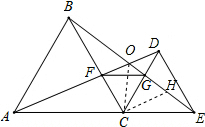 ∵∠AOB+∠ABO+∠BAO=180°,∠OBC=∠CAO,
∵∠AOB+∠ABO+∠BAO=180°,∠OBC=∠CAO,
∴∠AOB+∠ABC+∠BAC=180°,
∴∠AOB=60°,
∵∠EOD+∠EDO+∠OED=180°,
∴∠ODC+∠DEO=60°,
∴∠ODC=∠CEO,
同理∠OCD=∠DEO,
∴∠COE=60°,
同理∠AOC=60°,
∴∠AOC=∠EOC;故③正确;
∵∠FGD+∠DFG+∠FDG=180°,
∵∠DFG=∠DEO,∠FDG=∠CEO,
∴∠DFG+∠FDG=60°
∴∠FGD=∠ACD=120°,
∴PQ∥AE,故②正确;
∵FG∥AE
∴∠CFG=∠ACB=60°,
∵∠FCG=60°,
∴△CFG为等边三角形,
∴CF=CG,
在△ACF与△BCG中,
$\left\{\begin{array}{l}{AC=AC}\\{∠ACB=∠BCG}\\{CF=CG}\end{array}\right.$,
∴△ACF≌△BCG,
∴AF=BG;故①正确;
故答案为:①②③;
(3)在OE上截取OH=OC,
∵∠COE=60°,
∴OC=OH=CH,
∴∠OCH=60°,
∴∠OCG=∠HCE,
在△OCD与△HCE中,
$\left\{\begin{array}{l}{OC=HC}\\{∠OCD=∠HCE}\\{CD=CE}\end{array}\right.$,
∴△OCD≌△HCE,
∴HE=OD,
∵OE=OH+HE,
∴OE=OC+OD.
点评 本题考查了全等三角形的判定,考查了全等三角形的对应边、对应角相等的性质,考查了平行线的运用,考查了正三角形的判定,正确的作出辅助线是解题的关键.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
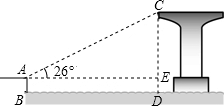 如图,岸边的点A处距水面的高度AB为2.17米,桥墩顶部点C距水面的高度CD为23.17米.从点A处测得桥墩顶部点C的仰角为26°,求岸边的点A与桥墩顶部点C之间的距离.(结果精确到0.1米)
如图,岸边的点A处距水面的高度AB为2.17米,桥墩顶部点C距水面的高度CD为23.17米.从点A处测得桥墩顶部点C的仰角为26°,求岸边的点A与桥墩顶部点C之间的距离.(结果精确到0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知一次函数y=-$\frac{1}{2}$x+b的图象经过点A(2,3),AB⊥x轴,垂足为B,连接OA.
如图,已知一次函数y=-$\frac{1}{2}$x+b的图象经过点A(2,3),AB⊥x轴,垂足为B,连接OA.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com