
 如图,已知一次函数y=-$\frac{1}{2}$x+b的图象经过点A(2,3),AB⊥x轴,垂足为B,连接OA.
如图,已知一次函数y=-$\frac{1}{2}$x+b的图象经过点A(2,3),AB⊥x轴,垂足为B,连接OA.分析 (1)将点A的坐标代入一次函数的解析式得:-$\frac{1}{2}$×2+b=3,解得b=4,求得一次函数的解析式为y=-$\frac{1}{2}x$+4,将y=0代入解得x=8,点C的坐标为(8,0);
(2)过点P作PD⊥OC,垂足为D.设点P的坐标为(x,-$\frac{1}{2}x+4$),则DP=$-\frac{1}{2}x+4$,由点A的坐标为(2,3)可知点B的坐标为(2,0),故此OB=2,由三角形的面积公式可知S=$-\frac{1}{2}x+4$;
(3)分为点M在x轴上和y轴上两种情况画出图形,然后再根据三角形的面积公式列出关于点M坐标的方程求解即可.
解答 解:(1)∵将x=2,y=3代入得:-$\frac{1}{2}$×2+b=3,解得:b=4,
∴一次函数的解析式为y=-$\frac{1}{2}x+4$.
∵将y=0代入得:$-\frac{1}{2}x+4$=0,解得x=8.
∴点C的坐标为(8,0).
(2)如图1所示:过点P作PD⊥OC,垂足为D.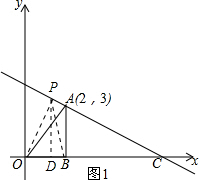
设点P的坐标为(x,-$\frac{1}{2}x+4$),则DP=$-\frac{1}{2}x+4$.
∵AB⊥OC,A(2,3),
∴点B(2,0).
∴OB=2.
∴${S}_{△POB}=\frac{1}{2}OB•PD$=$\frac{1}{2}×2×(-\frac{1}{2}x+4)$=-$\frac{1}{2}x+4$.
∴S=-$\frac{1}{2}x+4$(0<x<8).
(3)如图2所示: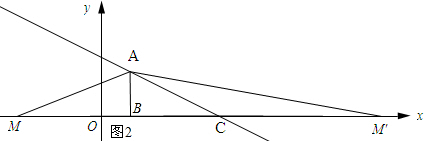
①当点M在x轴上且位于点C左侧时,设点M的坐标为(a,0),则MC=8-a.
∵S△MAC=24,
∴$\frac{1}{2}MC•AB=24$,即$\frac{1}{2}(8-a)×3=24$.
解得:a=-8.
∴点M的坐标为(-8,0).
②当点M位于点M′处时,设点M′的坐标为(a,0),则M′C=a-8.
∵S△MAC=24,
∴$\frac{1}{2}M′C•AB=24$,即$\frac{1}{2}(a-8)×3=24$.
解得:a=24.
∴点M的坐标为(24,0).
如图3所示:
∵将x=0代入y=-$\frac{1}{2}x+4$得:y=4.
∴点D的坐标为(0,4).
③当点M位于点D的下方时,设点M的坐标为(0,a),则DM=4-a.
∵S△ACM=S△MCD-S△MDA=24,
∴$\frac{1}{2}×(4-a)×8$-$\frac{1}{2}×(4-a)×2$=24.
解得:a=-4.
∴点M的坐标为(0,-4).
④当点M位于点M′处时,设点M的坐标为(0,a),则DM=a-4.
∵S△ACM=S△MCD-S△MDA=24,
∴$\frac{1}{2}×(a-4)×8-\frac{1}{2}×(a-4)×2$=24.
解得:a=12.
∴点M的坐标为(0,12).
综上所述,点M的坐标为M(-8,0)或M(24,0)或M(0,12)或M(0,-4).
点评 本题主要考查的是一次函数的综合应用、求函数的关系式、三角形的面积公式,根据题意画出图形,并根据三角形的面积公式列出关于a的方程是解题的关键.


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{4}{9}$ | B. | 1 | C. | $\frac{4}{9}$ | D. | 1或$\frac{4}{9}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
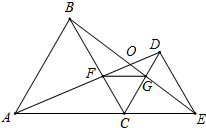 如图,点A,C,E在一条直线上,已知ABC和△EDC都是等边三角形,AD,BE相交于点O,AD,BC相交于点F,CD,BE相交于点G.连接FG和OC.
如图,点A,C,E在一条直线上,已知ABC和△EDC都是等边三角形,AD,BE相交于点O,AD,BC相交于点F,CD,BE相交于点G.连接FG和OC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
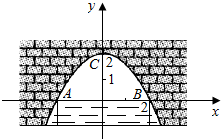 图中是抛物线形拱桥,当拱顶离水面2m时,水面宽4m,建立如图所示的平面直角坐标系:
图中是抛物线形拱桥,当拱顶离水面2m时,水面宽4m,建立如图所示的平面直角坐标系:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减(单位:个) | +5 | -2 | -5 | +15 | -10 | +16 | -9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com