
分析 (1)设这三张卡片上的数字为:x-6,x,x+6,根据题意列方程求解即可.
(2)因为卡片上的数字均为正整数,与(1)同法只需验证x是否为正整数即可.
解答 解:(1)设这三张卡片上的数字为:x-6,x,x+6
则:(x-6)+x+(x+6)=342,
3x=342
x=114
故:这三个数为:108,114,120
(2)小黄不可能拿到数字之和等于86的三张相邻的卡片,理由如下:
设这三张卡片上的数字为:x-6,x,x+6
小黄若拿到数字之和等于86,则:
(x-6)+x+(x+6)=86
3x=86
x=28$\frac{2}{3}$
因为卡片上的数字均为正整数,x不符合题意
所以,小黄不可能拿到数字之和等于86的三张相邻的卡片.
点评 本题考查了数字的变化规律问题,解题的关键是根据题意设未知数列方程.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
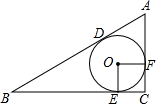 如图,⊙O是△ABC的内切圆,切点为D,E,F,∠C=90°,
如图,⊙O是△ABC的内切圆,切点为D,E,F,∠C=90°,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知双曲线y=$\frac{k}{x}$(x>0)经过矩形OABC的边AB,BC的中点F,E,且四边形OEBF的面积为2,求k的值.
如图,已知双曲线y=$\frac{k}{x}$(x>0)经过矩形OABC的边AB,BC的中点F,E,且四边形OEBF的面积为2,求k的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com