
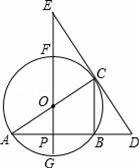
如图,⊙O中,FG、AC是直径,AB是弦,FG⊥AB,垂足为点P,过点C的直线交AB的延长线于点D,交GF的延长线于点E,已知AB=4,⊙O的半径为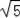
 .
.
(1)分别求出线段AP、CB的长;
(2)如果OE=5,求证:DE是⊙O的切线;
(3)如果tan∠E=
 ,求DE的长.
,求DE的长.

【考点】切线的判定.
【专题】证明题.
【分析】(1)根据圆周角定理由AC为直径得∠ABC=90°,在Rt△ABC中,根据勾股定理可计算出BC=2,再根据垂径定理由直径FG⊥AB得到AP=BP=
 AB=2;
AB=2;
(2)易得OP为△ABC的中位线,则OP=
 BC=1,再计算出
BC=1,再计算出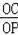
 =
=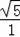
 =
=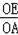
 ,根据相似三角形的判定方法得到△EOC∽△AOP,根据相似的性质得到∠OCE=∠OPA=90°,然后根据切线的判定定理得到DE是⊙O的切线;
,根据相似三角形的判定方法得到△EOC∽△AOP,根据相似的性质得到∠OCE=∠OPA=90°,然后根据切线的判定定理得到DE是⊙O的切线;
(3)根据平行线的性质由BC∥EP得到∠DCB=∠E,则tan∠DCB=tan∠E=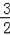
 ,在Rt△BCD中,根据正切的定义计算出BD=3,根据勾股定理计算出CD=
,在Rt△BCD中,根据正切的定义计算出BD=3,根据勾股定理计算出CD=
 ,然后根据平行线分线段成比例定理得
,然后根据平行线分线段成比例定理得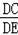
 =
=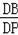
 ,再利用比例性质可计算出DE=
,再利用比例性质可计算出DE=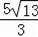
 .
.
【解答】(1)解:∵AC为直径,
∴∠ABC=90°,
在Rt△ABC中,AC=2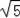
 ,AB=4,
,AB=4,
∴BC=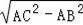
 =2,
=2,
∵直径FG⊥AB,
∴AP=BP=
 AB=2;
AB=2;
(2)证明∵AP=BP,AO=OC
∴OP为△ABC的中位线,
∴OP=
 BC=1,
BC=1,
∴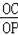
 =
=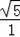
 ,
,
而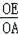
 =
=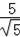
 =
=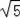
 ,
,
∴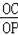
 =
=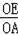
 ,
,
∵∠EOC=∠AOP,
∴△EOC∽△AOP,
∴∠OCE=∠OPA=90°,
∴OC⊥DE,
∴DE是⊙O的切线;
(3)解:∵BC∥EP,
∴∠DCB=∠E,
∴tan∠DCB=tan∠E=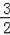

在Rt△BCD中,BC=2,tan∠DCB=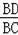
 =
=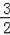
 ,
,
∴BD=3,
∴CD=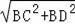
 =
=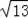
 ,
,
∵BC∥EP,
∴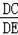
 =
=
 ,即
,即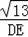
 =
=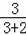
 ,
,
∴DE=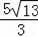
 .
.
【点评】本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.也考查了垂径定理、圆周角定理、勾股定理和相似三角形的判定与性质.


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com